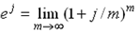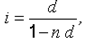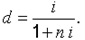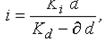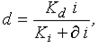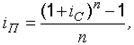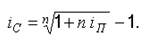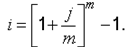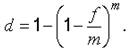Определение срока ссуды и размера процентной ставки
Наряду с расчетом будущей и современной величины денежных средств часто возникают задачи определения других параметров финансовых операций: их продолжительности и величины процентной или учетной ставок. Например, может возникнуть вопрос: сколько времени понадобится, чтобы данная сумма при заданном уровне процентной ставки удвоилась, или при каком уровне учетной ставки в течение года исходная сумма возрастет в полтора раза? Решение подобных задач сводится к преобразованию соответствующей формулы наращения (дисконтирования) таким образом, чтобы вычислить значение неизвестного параметра. Например, если надо рассчитать продолжительность ссуды по известным первоначальной и будущей суммам, а также уровню простой процентной ставки, то преобразуя формулу начисления простых декурсивных процентов (S = P * (1 + ni)), получим формулу (5) из табл. 1. (Все формулы и их нумерация приведены в табл. 1).
По такой же формуле будет определяться срок до погашения обязательства при математическом дисконтировании.
Определение срока финансовой операции для антисипативного начисления процентов и банковского учета производится по формуле (1) из табл. 1. Например, нужно определить через какой период времени произойдет удвоение суммы долга при начислении на нее 20% годовых простых а) при декурсивном методе начисления процентов; б) при использовании антисипативного метода. Временная база в обоих случаях принимается равной 365 дней (точные проценты).
Применив формулы (1) и (2), получим:
- а) t = (2 – 1) / 0,2 * 365 = 1825 дней (5 лет);
б) t = (1 – 1 / 2) / 0,2 * 365 = 912,5 дней (2,5 года)
Эти же формулы можно применить для определения срока до погашения обязательств при дисконтировании. Например, по векселю номиналом 700 тыс. рублей банк выплатил 520 тыс. рублей, произведя его учет по простой ставке 32% годовых. Чему равен срок до погашения векселя? Применив формулу (2), получим:
t = (1 – 520 / 700) / 0,32 * 360 = 289 дней
Товар, стоимостью 1,5 млн. рублей оплачивается на условиях коммерческого кредита, предоставленного под 15% годовых (простая процентная ставка, временная база 360 дней).
Сумма оплаты по истечении срока кредита составила 1 млн. 650 тыс. рублей. Чему равен срок предоставленного кредита? Из формулы (1) следует:
Вклады Сбербанка и их процентная ставка
... Сберегательный Сертификат на ответственное хранение в Сбербанке Процентные ставки по Сберегательному Сертификату Сбербанка , % годовых , срок (дни) Процентные ставки по вкладам , % годовых, Вклад «Сохраняй» 1000- 100 000 ... с доходов по вкладу не взимается. Преимущества вкладов Сбербанка: - для открытия вклада достаточно всего 1000 рублей - индивидуальный срок вклада с точностью до дня - начисление ...
t = (1,65 / 1,5 – 1) / 0,15 * 360 = 240 дней
Таблица 1
Формулы расчета продолжительности финансовых операций и процентных (учетных) ставок по ним
|
Способ начисления процентов |
Продолжительность ссуды |
Процентная (учетная) ставка |
|
1. Простые декурсивные проценты (t – длительность в днях, K – временная база) |
(1) |
(7) |
|
2. Простые антисипативные проценты (t – длительность в днях, K – временная база) |
(2) |
(8) |
|
3. Сложные декурсивные проценты проценты по эффективной ставке i (n — лет) |
(3) |
(9) |
|
4. Сложные декурсивные проценты по номинальной ставке j (n — лет) |
(4) |
(10) |
|
5. Дисконтирование по сложной эффективной учетной ставке d (n – длительность, лет) |
(5) |
(11) |
|
6. Дисконтирование по сложной номинальной учетной ставке f (n – лет) |
(6) |
(12) |
|
Непрерывное наращение (дисконтирование) по постоянной силе роста (n – лет)d |
(7) |
(19) |
Например, сколько лет должен пролежать на банковском депозите под 20% (сложная процентная ставка i) вклад 100 тыс. рублей, чтобы его сумма составила 250 тыс. рублей? Подставив данные в формулу (3), получим:
n = log2(250 / 100) / log2(1 + 0,2) ≈ 5 лет
Если начисление процентов при этих же условиях будет производиться ежемесячно, то в соответствии с формулой (4):
n = log2(250 / 100) / log2(1 + 0.2 / 12)12 ≈ 4,6 года
Чтобы избежать использования вычислений логарифмов, разработаны упрощенные способы приближенных вычислений срока финансовых операций. Один из них — “правило 70” — позволяет определить период удвоения первоначальной суммы при начислении сложных процентов по приближенной формуле 70% / i. Проверим его на нашем примере, заменив значение наращенной суммы 250 тыс. рублей на 200 тыс. рублей. По “правилу 70” эта сумма должна быть накоплена через 3,5 года (0,7 / 0,2).
Подставив соответствующие значения в формулу (3) получим 3,8 года.
Еще одним важнейшим параметром любой финансовой операции является процентная (учетная) ставка. Кроме технической функции, выполняемой этим показателем в ходе расчетов, он используется для оценки доходности – одного из фундаментальных понятий финансового менеджмента.
Сталкиваясь с упоминанием о процентных ставках, необходимо выяснить о каких процентах – простых или сложных, дискретных или непрерывных, – идет речь. Далее необходимо точно определиться с временной базой – рассчитываются ли годовые проценты или какие-то еще, если проценты годовые, то возникает вопрос, каким образом определяется длительность операции и продолжительность года. В случае начисления сложных процентов должно быть оговорено количество начислений процентов в течение года.
Вначале рассмотрим способы расчета величины процентных (учетных) ставок, когда заданы другие параметры финансовой операции. Преобразовав формулы декурсивного и антисипативного наращения простых процентов, получим выражения (7) и (8) в табл.1).
Например, чему будет равна простая процентная ставка по ссуде, выданной на 90 дней в размере 350 тыс. рублей, и возвращенной по истечении срока в сумме 375 тыс. рублей (временная база 360 дней)? Подставив эти данные в формулу (7), получим:
i = (375 – 350) / (350 * 90) * 360 ≈ 28,6%
Вексель номиналом 1 млн. рублей учтен в банке за 60 дней до его погашения в сумме 900 тыс. рублей. По какой простой учетной ставке было произведено его дисконтирование? Используем для расчетов формулу (8):
d = (1 – 0,9) / (1 * 60) * 360 = 60%
Не следует отождествлять процентную ставку, указываемую в кредитном договоре, с доходностью операции, рассчитанной в процентах. В первом случае процентная ставка является реальным параметром финансовой операции, однозначно определяющим величину платежа, который должен последовать в случае исполнения договора. Доходность же – это производная величина, не определяющая, а определяемая теми денежными потоками, которые порождает кредитный договор (ценная бумага или другой финансовый инструмент).
Рассчитывая доходность финансовой операции, инвестор получает субъективную оценку ее величины, зависящую от целого ряда предпосылок, таких как способ начисления процентов, выбор временной базы и т.п. Эти предпосылки не являются объективными и неизбежными.
Чтобы не запутаться в обилии методов расчета процентных ставок, достаточно четко представлять, каким образом она получена. Кроме этого, следует помнить, что любому значению данной ставки может быть поставлено в соответствие эквивалентное значение какой-либо другой процентной или учетной ставки. Эквивалентными называются ставки, наращение или дисконтирование по которым приводит к одному и тому же финансовому результату.
Непрерывное наращение и дисконтирование, непрерывные проценты
Для непрерывных процентов не существует различий между процентной и учетной ставками, поскольку сила роста – универсальный показатель. Однако наряду с постоянной силой роста может использоваться переменная процентная ставка, величина которой меняется по заданному закону (математической функции).
Непрерывное начисление процентов используется при анализе сложных финансовых задач, например, обоснование и выбор инвестиционных решений. Оценивая работу финансового учреждения, где платежи за период поступают многократно, целесообразно предполагать, что наращенная сумма непрерывно меняется во времени и применять непрерывное начисление процентов.
Все ситуации, которые мы до сих пор рассматривали, относились к дискретным процентам, поскольку их начисление осуществляется за фиксированные промежутки времени (год, квартал, месяц, день, час).
Но на практике нередко встречаются случаи, когда проценты начисляются непрерывно, за сколь угодно малый промежуток времени. Если бы проценты начислялись ежедневно, то годовой коэффициент (множитель) наращения выглядел так:
|
kн = (1 + j / m)m = (1 + j / 365)365 |
(1) |
Но поскольку проценты начисляются непрерывно, то m стремится к бесконечности, а коэффициент (множитель) наращения стремится к e j:
|
|
(2) |
где e ≈ 2,718281, называется числом Эйлера и является одной из важнейших постоянных математического анализа.
Отсюда можно записать формулу наращенной суммы для n лет:
|
FV = PV
|
(3) |
Ставку непрерывных процентов называют силой роста (force of interest) и обозначают символом δ, в отличие от ставки дискретных процентов ( j ).
Пример. Кредит в размере на 100 тыс. долларов получен сроком на 3 года под 8% годовых. Определить сумму подлежащего возврату в конце срока кредита, если проценты будут начисляться:
- а) один раз в год;
- б) ежедневно;
- в) непрерывно.
Решение:
Используем формулы дискретных и непрерывных процентов:
начисление один раз в год
FV = 100’000
- (1 + 0,08)3 = 125’971,2 долларов;
ежедневное начисление процентов
FV = 100’000
- (1 + 0,08 / 365)365
- 3 = 127’121,6 долларов
непрерывное начисление процентов
FV = 100’000
- e0,08
- 3 = 127’124,9 долларов.
Средние процентные ставки, эквивалентность процентных ставок (эквивалентность простых и сложных ставок, эквивалентность сложных дискретных и непрерывных ставок)
При проведении различных финансовых операций в расчетах могут использоваться различные виды процентных ставок, поэтому для сравнения доходности (эффективности) таких операций необходимо уметь по заданному значению процентной ставки одного вида определять эквивалентное значение процентной ставки другого вида.
Две процентные ставки называют эквивалентными, если их применение к одинаковым суммам в течение равных промежутков времени в однотипных по назначению операциях дает одинаковые финансовые результаты.
Расчет эквивалентных ставок сводится к следующему алгоритму:
- выбор величины, рассчитываемой при помощи различных ставок (наращенной суммы, суммы процентных денег и др.);
- составление уравнения эквивалентности на основе равенства двух формул, определяющих выбранную величину;
- вывод формулы эквивалентности процентных ставок из уравнения эквивалентности.
Эквивалентные значения простой ставки процентов и учетной ставки определяются соотношениями:
|
|
(1) |
|
|
(2) |
Если сроки операций заданы в днях, эти формулы примут вид:
|
|
(3) |
|
|
(4) |
где – расчетное количество дней в году при начислении процентов; – расчетное количество дней в году при учете векселей.
Пример. Вексель учтен в банке по простой учетной ставке 20 % годовых за 90 дней до срока его погашения. Определить значение эквивалентной ставки простых процентов, определяющей доходность операции учета, если расчетное количество дней в году при учете векселей принимается равным 360, а при начислении процентов – равным 365.
Решение
По приведенной выше формуле
0,21 или 21 %.
Эквивалентные значения простой и сложной годовых ставок процентов определяются соотношениями:
|
|
(5) |
|
|
(6) |
Годовая ставка сложных процентов, эквивалентная номинальной годовой ставке процентов при их начислении несколько раз в году, определяется по формуле:
|
|
(7) |
Такая ставка называется эффективной процентной ставкой. Она показывает, какая годовая ставка процентов дает тот же финансовый результат, что и m-разовое начисление процентов по ставке j/m.
Пример. Банк начисляет сложные проценты на вклады по номинальной ставке 120 % годовых. Определить доходность вкладов по годовой ставке процентов при их ежемесячном начислении.
Решение
По приведенной выше формуле
i = (1 + 1,2 / 12) 12 – 1 = 2,14 или 214 %.
Аналогично эффективная учетная ставка характеризует результат дисконтирования за год и определяется по формуле:
|
|
(8) |
Финансовая математика – раздел количественного анализа финансовых операций, предметом которого является изучение функциональных зависимостей между параметрами коммерческих сделок или финансово-банковских операций и разработка на их основе методов решения финансовых задач определенного класса.
Фактор времени играет огромную роль и определяется принципом неравноценности денег, относящимся к разным моментам времени. Сегодняшние деньги ценнее будущих по следующим причинам:
- во-первых, деньги можно продуктивно использовать во времени как приносящий доход финансовый актив, т.е. деньги могут быть инвестированы, и тем самым принести доход. Рубль в руке сегодня стоит больше, чем рубль, который должен быть получен завтра ввиду процентного дохода, который вы можете получить, положив его на сберегательный счет или проведя другую инвестиционную операцию;
- во-вторых, инфляционные процессы ведут к обесцениванию денег во времени. Сегодня на рубль можно купить товара больше, чем завтра на этот же рубль, т.к. цены на товар повысятся;
- в-третьих, неопределенность будущего и связанный с этим риск повышает ценность имеющихся денег. Сегодня рубль в руке уже есть и его можно израсходовать на потребление, а будет ли он завтра в руке, – еще вопрос.
Относительный показатель, характеризующий интенсивность начисления процентов за единицу времени, – процентная ставка. Методика расчета проста: отношение суммы процентных денег, выплачивающихся за определенный период времени, к величине ссуды. Этот показатель выражается либо в долях единицы, либо в процентах. Таким образом, процентная ставка показывает, сколько денежных единиц должен заплатить заемщик за пользование в течение определенного периода времени 100 единицами первоначальной суммы долга.
Список использованной литературы
- Бухвалов А., Бухвалова В., Идельсон А. Финансовые вычисления для профессионалов. СПб.: БХВ-Петербург, 2006. – 320 с.
- Ершов Ю.С. Финансовая математика, ООО «Бизнес ПРАКТИКА», Новосибирск, 2008. – 212 с.
- Малыхин В.И. Финансовая математика. М.: ЮНИТИ-ДАНА, 2002. – 247 с.
- Малюгин В.И. Рынок ценных бумаг: Количественные методы анализа. Мн.: БГУ, 2007. – 318 с.
- Просветов Г.И. Финансовый менеджмент: задачи и решения. М: Альфа-Пресс, 2007. – 340 с.
- Четыркин Е.М. Финансовая математика. М.: Дело, 2002. – 400 с.
- Ширяев А.Н. Основы стохастической и финансовой математики. Т.1. Факты. Модели. М.: ФАЗИС, 2008. — 489 с.
Задача 9
Условие задачи 8:
Компания по производству радиоаппаратуры получила в коммерческом банке ссуду в 90000 р. на два года под простой дисконт, равный 12% в год. Какую сумму получила компания на руки?
Условие задачи 9:
Компания из упражнения 8 желает получить при тех же условиях на руки 90 000 р. Какую сумму (будущую стоимость) она будет должна банку?
Решение :
Решение задачи 8:
Расчеты при применении простого дисконта производятся по формуле:
Р = 90 000 * (1 — 0,12 * 2) = 68 400 руб.
Ответ: Компания получила на руки сумму = 68 400 руб.
Решение задачи 9:
Определим сумму (будущую стоимость) которую компания будет должна банку по формуле: Преобразуя формулу (1), получаем:
S = 90 000 / (1 — 0,12 * 2) = 118 421,1 руб.
Ответ : сумму (будущую стоимость) которую компания будет должна банку = 118 421,1 руб.
Задача 39
Допустим, рассматривается проект стоимостью 100 млн. р. Ожидается, что ежемесячные доходы по проекту составят 16, 25, 36, 49 млн. р. за четыре месяца. Определите чистую текущую стоимость проекта, если годовая ставка процента 19%.
Решение :
Если капитальные вложения, связанные с предстоящей реализацией проекта, осуществляют в несколько этапов (интервалов), то расчет показателя NPV производят по следующей формуле:
— где NPV — чистая текущая стоимость;
— CFt — приток денежных средств в период t;
— It — сумма инвестиций (затраты) в t-ом периоде;
— r — барьерная ставка (ставка дисконтирования);
— n — суммарное число периодов (интервалов, шагов) t = 1, 2, …, n (или время действия инвестиции).
NPV=-100 + 16/(1+0,19)^(1/12) +25/(1+0,19)^(2/12) +36/(1+0,19)^(3/12) +49/(1+0,19)^(4/12) =20,76288 млн.руб.
Ответ : чистая те¬кущая стоимость проекта = 20,76288 млн.руб.
Задача 69
Срок ссуды — 5 лет, договорная базовая процентная ставка — 12 % годовых плюс маржа 0,5 % в первые два года и 0,75 % в оставшиеся годы. Определить множитель наращения.
Решение :
S=〖(1+0,125)〗^2*〖(1+0,1275)〗^3=1,81407.
Ответ : Множитель наращения = 1,81407.
Задача 99
Рассчитайте ежегодный платеж за аренду оборудования стоимостью $10000 в течение 10 лет, если к концу аренды остаточная стоимость оборудования будет $5000. Норматив доходности принять равным 15 %.
Решение :
Определение размера платежа за аренду оборудования может быть выполнено по следующей схеме:
R= (P-S*v^n)/a_ni =(10 000-5 000*(1/(1+0,15)^10 ))/((1-(1+0,15)^(-10))/0,15)=(10 000-5 000*0,247185)/5,018769=(10 000-1235,924)/5,018769=1 746,26 $.
Ответ : ежегодный платеж за аренду оборудования = 1 746,26 $.
Задача 129
При выдаче ссуды на 180 дней под 8% годовых кредитором удержаны комиссионные в размере 0,5% суммы кредита. Какова эффективность ссудной операции в виде годовой ставки сложных процентов?
Решение :
— I_э=√(180/365&(1+180*0,08/365)/(1-0,4/100))-1=0,08185 или 8,185%
Ответ : Эффективность ссудной операции = 8,185%.
Задача 18
Фермер хочет вложить 30 000 р., чтобы через 5 лет получить 40 000 р. Под какую процентную ставку j12 он должен вложить свои деньги?
Решение :
i=((S/P)^(1/nm)-1)*m=(((40 000)/(30 000))^(1/(5*12))-1)*12=0,0577 или 5,77%.
Ответ : Фермер должен вложить 30 000 р. под процентную ставку = 5,77%.
Задача 48
Определите эффективность инвестиций размером 200 млн. р., если ожидаемые ежемесячные доходы за первые пять месяцев составят соответственно: 20, 40, 50, 80 и 100 млн. р. Издержки привлечения капитала составляют 13,5% годовых.
Решение :
NPV — это сумма денежных потоков, связанных с данным инвестиционным решением, приведенная по фактору времени к моменту оценки, т.е.
где СFj — денежный поток, приуроченный к j-му моменту (интервалу) времени;
— n — срок жизни проекта.
Срок операции n в общем случае измеряется в годах. Если же реальная операция не отвечает этим условиям, т.е. интервалы между платежами не равны году, то в качестве единицы измерения срока принимаются доли года, измеренные как правило в месяцах, деленных на 12.
Интерпретация NPV.
NPV > О означает следующее:
— выраженный в “сегодняшней” оценке эффект от проекта составляет положительную величину;
— проект имеет доходность более высокую, чем ставка дисконта r, требуемая на рынке капиталов от инвестиций с таким уровнем риска.
Таким образом, данный критерий идеально подходит для оценки отдельных инвестиционных проектов, абсолютной величины их эффекта.
Тогда в цифрах решение задачи:
NPV = — 200 + + + + + + = 78,95 (млн.руб.)
Индекс прибыльности (profitability index, PI) показывает относительную прибыльность проекта, или дисконтированную стоимость денежных поступлений от проекта в расчете на единицу вложений. Он рассчитывается путем деления чистых приведенных поступлений от проекта на стоимость первоначальных вложений:
Индекс прибыльности проекта:
— PI = 78,95 / 200 = 0,39 < 1, следовательно проект эффективен.
Учитывая, что NPV = 78,95 (млн.руб.) > 0, IRR = 244,4% годовых можно сделать вывод – проект эффективен.
Задача 78
Платежи в 1 и 2 млн. р. и сроками уплаты через 2 и 3 года объединяются в один со сроком 2,5 года. При консолидации используется сложная ставка 20 %. Найти искомую сумму.
Решение :
FV=1*〖(1+0,2)〗^(2.5-2)+2*〖(1+0,2)〗^(2.5-3)=2,921187 млн.руб.
Ответ: искомая сумма = 2,921187 млн. руб.
Задача 108
Вы разместили средства в виде трехмесячного депозита под ставку 20% годовых простых процентов. Но темп инфляции составил 15 % годовых. Какова реальная ставка процентов?
Решение :
Определяется по формуле Фишера: r = i + h + i h
где r – процентная ставка с поправкой на инфляцию;
i – простая ставка процентов, характеризующая требуемую реальную
доходность финансовой операции (нетто-ставка);
— h — показатель инфляции.
Индекс цен: J_p=(1+h)^n=(1+0,15)^(3/12)=1,035558.
Ставка процентов по кредиту с учетом инфляции должна быть равна:
r=0,2+0,15+0,2*0,15=0,38.
При начислении простых процентов годовая реальная ставка процентов равна
i= 1/n*((1+nr)/J_p -1)=1/(3/12)*((1+3/12*0,38)/1,035558-1)=0,229603 или 22,96%.
Ответ : Реальная ставка процентов = 0,229603 или 22,96%.
Задача 43
Рассчитайте текущую стоимость вклада, который через три года составит 15000 тыс. р. при ставке процента 20% годовых.
Решение :
РV=15 000/(1+0,2)^3 =8680,556 тыс.руб.
Ответ : Текущая стоимость вклада = 8680,556 тыс. руб.
не сложно
Важно! Все представленные Рефераты для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Если Реферат, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, об этом нам.