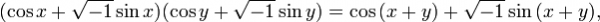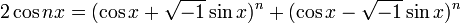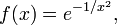Математический анализ

метки: Анализ, Функция, Математический, Дифференциальный, Математик, Теория, Лопиталь, Исчисление

Введение, Математи́ческий ана́лиз

В учебном процессе к анализу относят

• дифференциальное и интегральное исчисление;
• теорию рядов (функциональных, степенных и Фурье) и многомерных интегралов;
• векторный анализ.

При этом элементы функционального анализа и теории интеграла Лебега даются факультативно, а ТФКП, вариационное исчисление, теория дифференциальных уравнений читаются отдельными курсами. Строгость изложения следует образцам конца XIX века и в частности использует наивную теорию множеств.

Программа курса анализа, читаемого в университетах РФ, примерно соответствует программе англо-американского курса «Calculus» ^[1] .

1. История

исчисление бесконечно малых

«Новый метод максимумов и минимумов…»

1.1. Лейбниц и его ученики

Анализ бесконечно малых

Бесконечно малая часть, на которую непрерывно увеличивается или уменьшается переменная величина, называется ее дифференциалом… Для обозначения дифференциала переменной величины, которая сама выражается одной буквой, мы будем пользоваться знаком или символом d .^[5] … Бесконечно малая часть, на которую непрерывно увеличивается или уменьшается дифференциал переменной величины, называется … вторым дифференциалом.^[6]

Эти определения поясняются геометрически, при этом на рис. бесконечно малые приращения изображены конечными. Рассмотрение опирается на два требования (аксиомы).

Первое:

Требуется, чтобы две величины, отличающиеся друг от друга лишь на бесконечно малую величину, можно было брать [при упрощении выражений?] безразлично одну вместо другой. ^[7]

Отсюда получается x + dx = x , далее

dxy = (x + dx )(y + dy ) − xy = xdy + ydx + dxdy = (x + dx )dy + ydx = xdy + ydx

и проч. правила дифференцирования. Второе требование гласит:

Анализ финансовых результатов и совершенствование деятельности ...

... на основе изучения финансовых результатов его работы [15, c.89]. Прибыль и есть финансовый результат деятельности предприятия, характеризующий абсолютную эффективность его работы [16, с.229]. Прибыль является конечным результатом деятельности предприятия. В современной экономической науке термин ...

Требуется, чтобы можно было рассматривать кривую линию как совокупность бесконечного множества бесконечно малых прямых линий. ^[8]

Продолжение каждой такой линии называется касательной к кривой. ^[9] Исследуя касательную, проходящую через точку M = (x ,y ) , Лопиталь придаёт большое значение величине

,

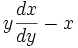достигающее экстремальных значений в точках перегиба кривой, отношению же dy к dx не придаётся никакого особого значения.

Примечательно нахождение точек экстремума. Если при непрерывном увеличении диаметра x ордината y сначала возрастает, а затем убывает, то дифференциал dy сначала положителен по сравнению с dx , а потом отрицателен.

Но всякая непрерывно возрастающая или убывающая величина не может превратиться из положительной в отрицательную, не проходя через бесконечность или нуль… Отсюда следует, что дифференциал наибольшей и наименьшей величины должен равняться нулю или бесконечности. ^[10]

Вероятно, эта формулировка не безупречна, если вспомнить о первом требовании: пусть, скажем, y = x ² , тогда в силу первого требования

2xdx + dx ² = 2xdx ;

в нуле правая часть равна нулю, а левая нет. Видимо следовало сказать, что dy можно преобразовать в соответствии с первым требованием так, чтобы в точке максимума dy = 0 .^[11] . В примерах все само собой понятно, и лишь в теории точек перегиба Лопиталь пишет, что dy равен нулю в точке максимума, будучи разделён на dx ^[10] .

Далее, при помощи одних дифференциалов формулируются условия экстремума и рассмотрено большое число сложных задач, относящихся в основном к дифференциальной геометрии на плоскости. В конце книги, в гл. 10, изложено то, что теперь называют правилом Лопиталя, хотя и в не совсем обычной форме. Пусть величина ординаты y кривой выражена дробью, числитель и знаменатель которой обращаются в нуль при x = a . Тогда точка кривой с x = a имеет ординату y , равную отношению дифференциала числителя к дифференциалу знаменателя, взятому при x = a .

Математических лекциях о методе интеграла

Указывая на практическую полезность и простоту нового метода Лейбниц писал:

То, что человек, сведущий в этом исчислении, может получить прямо в трёх строках, другие учёнейшие мужи принуждены были искать, следуя сложными обходными путями.

1.2. Эйлер

аналитическое выражение

Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этой переменного количества и чисел или постоянных количеств. ^[15]

14 стр., 6929 слов

Кривые «доход-потребление» и кривые Энгеля

... с помощью кривых Энгеля и кривых «доход-потребление». Научная новизна дипломной работы заключается в исследовании влияния кривых Энгеля и кривых «доход ... ними в процессе производства, распределения, обмена, потребления. Теория потребления ... иных потребностей. По мере роста благ, их наличного количества полезность обесценивается. ... Данные предпочтения являются «чистыми», так как не зависят от доходов и ...

Подчёркивая, что «основное различие функций лежит в способе составления их из переменного и постоянных», Эйлер перечисляет действия, «посредством которых количества могут друг с другом сочетаться и перемешиваться; действиями этими являются: сложение и вычитание, умножение и деление, возведение в степень и извлечение корней; сюда же следует отнести также решение [алгебраических] уравнений. Кроме этих действий, называемых алгебраическими, существует много других, трансцендентных, как-то: показательные, логарифмические и бесчисленные другие, доставляемые интегральным исчислением». ^[16] Такая трактовка позволяла без труда обращаться с многозначными функциями и не требовала пояснения, над каким полем рассматривается функция: выражение для счёта определено для комплексных значений переменных даже тогда, когда для рассматриваемой задачи это не нужно.

Операции в выражении допускались лишь в конечном числе, а трансцендентное проникало при помощи бесконечно большого числа ^[17] . В выражениях это число используется наряду с натуральными числами. Напр., считается допустимым такое выражение для экспоненты

,

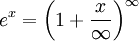в котором лишь поздние авторы видели предельный переход. С аналитическими выражениями производились разнообразные преобразования, позволившие Эйлеру найти представления для элементарных функций в виде рядов, бесконечных произведений и т. д. Эйлер преобразует выражения для счёта так, как это делают в алгебре, не обращая внимания на возможность вычислить значение функции в точке по каждой из написанных формул.

В отличие от Лопиталя Эйлер подробно рассматривает трансцендентные функции и в особенности два наиболее изученные их классы — показательные и тригонометрические. Он обнаруживает, что все элементарные функции могут быть выражены при помощи арифметических действий и двух операций — взятия логарифма и экспоненты ^[18] .

Сам ход доказательства прекрасно демонстрирует технику использования бесконечно большого. Определив синус и косинус при помощи тригонометрического круга, Эйлер выводит из формул сложения следующее:

а отсюда

Полагая и z = nx , он получает

,

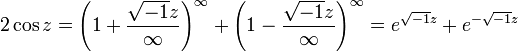отбрасывая бесконечно малые величины большего порядка. Используя это и аналогичное выражение, Эйлер получает и свою знаменитую формулу

.

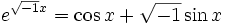Указав различные выражения для функций, которые теперь называют элементарными, Эйлер переходит к рассмотрению кривых на плоскости, начертанным свободным движением руки. По его мнению, не для всякой такой кривой можно отыскать единое аналитическое выражение).

Анализ хозяйственной деятельности

... мы попытаемся познать объективное содержание хозяйственной деятельности. 1.Теория анализа ФХД 1.1 Цели и принципы анализа ФХД Содержанием АФХД является глубокое и всестороннее изучение экономической информации о функционировании анализируемого субъекта ...

^[19] В XIX веке с подачи Казорати^[20] это утверждение считалось ошибочным: по теореме Вейерштрасса всякая непрерывная в современном смысле кривая может быть приближенно описана полиномами. На самом деле Эйлера это едва ли убедило, ведь нужно ещё переписать предельный переход при помощи символа .

Изложение дифференциального исчисления Эйлер начинает с теории конечных разностей, за ним в третьей главе следует философское разъяснение о том, что «бесконечно малое количество есть точно нуль», более всего не устроившее современников Эйлера. Затем из конечных разностей при бесконечно малом приращении образуются дифференциалы, а из интерполяционной формулу Ньютона — формула Тейлора. Этот метод в существенном восходит к работам Тейлора (1715 г.).

При этом у Эйлера появляется устойчивое отношение 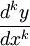, которое, однако, рассматривается как отношение двух бесконечно малых. Последние главы посвящены приближенному вычислению при помощи рядов.

В трёхтомном интегральном исчислении Эйлер трактует вводит понятие интеграла так:

Та функция, дифференциал которой = Xdx , называется его интегралом и обозначается знаком S , поставленным спереди.^[21]

В целом же эта часть трактата Эйлера посвящена более общей с современной точки зрения задаче об интегрировании дифференциальных уравнений. При этом Эйлер находит ряд интегралов и дифференциальных уравнений, которые приводят к новым функциям, напр., Γ -функции, эллиптические функции и т. д. Строгое доказательство их неэлементарности было дано в 1830-х годах Якоби для эллиптических функций и Лиувиллем (см. элементарные функции).

1.3. Лагранж

Теория аналитических функций

Желая избавиться от бесконечно малого вовсе, Лагранж обратил связь между производными и рядом Тейлора. Под аналитической функцией Лагранж понимал произвольную функцию, исследуемую методами анализа. Саму функцию он обозначил как f (x ) , дав графический способ записи зависимости — ранее же Эйлер обходился одними переменными. Для применения методов анализа по мнению Лагранжа необходимо, чтобы функция разлагалась в ряд

,

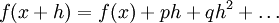коэффициенты которого будут новыми функциями x . Остаётся назвать p производной (дифференциальным коэффициентом) и обозначить его как f ‘(x ) . Таким образом, понятие производной вводится на второй странице трактата и без помощи бесконечно малых. Остаётся заметить, что

,

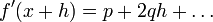поэтому коэффициент q является удвоенной производной производной f (x ) , то есть

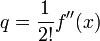и т. д.^[24]

Такой подход к трактовке понятия производной используется в современной алгебре и послужил основой для создания теории аналитических функций Вейерштрасса.

Анализ основных характеристик и функций облигаций на российском рынке

... Поэтому целью написания данной курсовой работы является раскрытие роли и функций облигаций, более детальное рассмотрение основных характеристик облигаций, а также анализ их доходности. Задачи, которые ... дохода, так и облигацияминового выпуска; облигации смешанного типа. Часть срока облигационного займавладелец облигации получает доход по фиксированной купоннойставке, а часть срока - по плавающей ...

Лагранж оперировал такими рядами как формальными и получил ряд замечательных теорем. В частности, впервые и вполне строго доказал разрешимость начальной задачи для обыкновенных дифференциальных уравнений в формальных степенных рядах. ^[25]

Теории аналитических функций, Алгебраическом анализе

доопределённую нулём в нуле. Эта функция всюду гладкая на вещественной оси и в нуле имеет нулевой ряд Маклорена, который, следовательно, не сходится к значению f (x ) . Против этого примера Пуассон возразил, что Лагранж определял функцию как единое аналитическое выражение, в примере Коши же функция задана по разному в нуле, и при 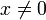. Лишь в конце XIX века Прингсхейм^[27] доказал, что существует бесконечно дифференцируемая функция, заданная единым выражением, ряд Маклорена для которой расходится. Пример такой функцией доставляет выражение

.

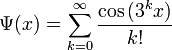1.4. Дальнейшее развитие

В XVIII веке были разработаны и практически применены такие разделы анализа, как вариационное исчисление, обыкновенные дифференциальные уравнения и дифференциальные уравнения в частных производных, преобразования Фурье и производящие функции. На фундаменте анализа возникла математическая физика, аналитические методы глубоко проникли в геометрию и даже в теорию чисел.

В XIX веке Коши первым дал анализу твёрдое логическое обоснование, введя понятие предела последовательности, он же открыл новую страницу комплексного анализа. Пуассон, Лиувилль, Фурье и другие изучали дифференциальные уравнения в частных производных и гармонический анализ.

В последней трети XIX века Вейерштрасс произвёл арифметизацию анализа, полагая геометрическое обоснование недостаточным, и предложил классическое определение предела через ε-δ-язык. Он же создал первую строгую теорию множества вещественных чисел. В это же время попытки усовершенствования теоремы об интегрируемости по Риману привели к созданию классификации разрывности вещественных функций. Также были открыты «патологические» примеры (нигде не дифференцируемые непрерывные функции, заполняющие пространство кривые).

В связи с этим Жордан разработал теорию меры, а Кантор — теорию множеств, и в начале XX века математический анализ был формализован с их помощью. Другим важным событием XX века стала разработка нестандартного анализа как альтернативного подхода к обоснованию анализа.

2. Разделы математического анализа

• Мера множества
• Функциональный анализ
• Гармонический анализ
• Комплексный анализ
• Нестандартный анализ
• Вычислительная математика
• Метрическое пространство, Топологическое пространство
• Аналитическая теория чисел
• Дифференциальные геометрия и топология

По курсу «Экономическая теория» «Функции экономической теории, ...

... считается американский ученый Т.Веблен. 2. Предмет экономической теории. Предмет экономической теории менялся по мере развития науки. Первоначально экономическая теория изучала только особенности домашнего хозяйства, затем ... различаются по целому ряду проблем. Однако можно выделить некоторые ведущие идеи этого течения: Институционалисты не замыкаются на анализе чисто экономических отношений, ...

3. Библиография

4.1. Энциклопедические статьи

• Анализ // Энциклопедический лексикон: Спб.: тип. А. Плюшара, 1835-1841. Том 1-17.

• Анализ математический // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.).

  — СПб. , 1890—1907.

4.1.2. Учебная литература

4.2.2.1. Стандартные учебники

На протяжении многих лет в России популярны следующие учебники:

• Курант, Р., Курс дифференциального и интегрального исчисления (в двух томах).

  Главная методическая находка курса: сначала попросту излагаются основные идеи, а затем им даются строгие доказательства. Написан Курантом в его бытность профессором Геттингенского университета в 1920-х под влиянием идей Клейна, затем в 1930-х перенесён на американскую почву. Русский перевод 1934 г. и его переиздания дает текст по немецкому изданию, перевод 1960-х годов (т. н. 4-ое издание) представляет собой компиляцию из немецкой и американской версии учебника и в связи с этим весьма многословен.

• Фихтенгольц, Григорий Михайлович. Курс дифференциального и интегрального исчисления (в трёх томах) и задачник
• Демидович, Б. П., Сборник задач и упражнений по математическому анализу
• Ляшко И. И. и др. Справочное пособие по высшей математике . т. 1-5

Некоторые ВУЗы имеют собственные руководства по анализу:

• МГУ, МехМат:

• Архипов Г. И., Садовничий В. А., Чубариков В. Н. Лекции по мат. анализу.
• Зорич В. А. Математический анализ. Часть I. М.: Наука, 1981. 544 с.
• Зорич В. А. Математический анализ. Часть II. М.: Наука, 1984. 640 с.
• Камынин Л. И. Курс математического анализа (в двух томах).

  М.: Издательство Московского Университета, 2001.

• В. А. Ильин , В. А. Садовничий , Бл. Х. Сендов . Математический анализ / Под ред. А. Н. Тихонова . — 3-е изд. , перераб. и доп. — М .: Проспект, 2006. — ISBN 5-482-00445-7

• МГУ, физфак:

• Ильин В. А., Позняк Э. Г. Основы математического анализа (в двух частях).

  — М .: Физматлит, 2005. — 648 с. — ISBN 5-9221-0536-1

• Бутузов В. Ф. и др. Мат. анализ в вопросах и задачах

• МГТУ им. Н. Э. Баумана:

• Математика в техническом университете Сборник учебных пособий в 21 томе.

• СПбГУ, физфак:

• Смирнов В. И. Курс высшей математики, в 5 томах. М.: Наука, 1981 (6-е издание), БХВ-Петербург, 2008 (24-е издание).
  4 стр., 1999 слов

  Примеры анализа рынков.Примеры бизнес-планов.Примеры выводов.Примеры ...

  ... соответственно в дипломе необходимо освятить все нормативно-правовые акты, которые регулируют банковскую деятельность, начертить структуру управления банковской деятельностью на федеральном, региональном и муниципальном уровнях, провести анализ деятельности банковского ...

• НГУ, мехмат:

• Решетняк Ю. Г. Курс математического анализа. Часть I. Книга 1. Введение в математический анализ. Дифференциальное исчисление функций одной переменной. Новосибирск: Изд-во Ин-та математики, 1999. 454 с ISBN 5-86134-066-8.
• Решетняк Ю. Г. Курс математического анализа. Часть I. Книга 2. Интегральное исчисление функций одной переменной. Дифференциальное исчисление функций многих переменных. Новосибирск: Изд-во Ин-та математики, 1999. 512 с ISBN 5-86134-067-6.
• Решетняк Ю. Г. Курс математического анализа. Часть II. Книга 1. Основы гладкого анализа в многомерных пространствах. Теория рядов. Новосибирск: Изд-во Ин-та математики, 2000. 440 с ISBN 5-86134-086-2.
• Решетняк Ю. Г. Курс математического анализа. Часть II. Книга 2. Интегральное исчисление функций многих переменных. Интегральное исчисление на многообразиях. Внешние дифференциальные формы. Новосибирск: Изд-во Ин-та математики, 2001. 444 с ISBN 5-86134-089-7.
• Шведов И. А. Компактный курс математического анализа, 2003: Часть 1. Функции одной переменной, Часть 2. Дифференциальное исчисление функций многих переменных.

• Физтех, Москва

• Кудрявцев Л. Д., Курс математического анализа (в трех томах).

• БГУ, физфак:

• Богданов Ю. С. Лекции по математическому анализу (в двух частях).

  — Минск: БГУ, 1974. — 357 с.

4.2.1.2.2. Учебники повышенной сложности

Учебники:

• Рудин У. Основы математического анализа. М., 1976 — небольшая книга, написана очень чётко и сжато.

Задачники повышенной сложности:

• Г.Полиа, Г.Сеге, Задачи и теоремы из анализа. Часть 1, Часть 2, 1978. (Большая часть материала относится к ТФКП)
• Pascal, E. (Napoli).

  Esercizii, 1895; 2 ed., 1909 // Internet Archiv

4.2.2.2.3. Учебники для гуманитариев

• А. М. Ахтямов Математика для социологов и экономистов. — М. : Физматлит, 2004.
• Н. Ш. Кремер и др. Высшая математика для экономистов. Учебник. 3-е изд. — М. : Юнити, 2010

4.2.3.2.4. Задачники

• Г. Н. Берман. Сборник задач по курсу математического анализа: Учебное пособие для вузов. — 20-е изд. М.:Наука. Главная редакция физико-математической литературы, 1985. — 384 с.
• П. Е. Данко, А. Г. Попов, Т. Я. Кожевников. Высшая математика в упражнениях и задачах. (В 2-х частях)- М.: Высш.шк, 1986.
• Г. И. Запорожец Руководство к решению задач по математическому анализу. — М.: Высшая школа, 1966.
• И. А. Каплан. Практические занятия по высшей математике, в 5 частях.. — Харьков, Изд. Харьковского гос. ун-та, 1967, 1971, 1972.
• А. К. Боярчук, Г. П. Головач. Диференциальные уравнения в примерах и задачах. Москва. Едиториал УРСС, 2001.
• А. В. Пантелеев, А. С. Якимова, А. В. Босов. Обыкновенные дифференциальные уравнения в примерах и задачах. «МАИ», 2000
• А. М. Самойленко, С. А. Кривошея, Н. А. Перестюк. Дифференциальные уравнения: примеры и задачи. ВШ, 1989.
• К. Н. Лунгу, В. П. Норин, Д. Т. Письменный, Ю.А Шевченко . Сборник задач по высшей математике. 1 курс. — 7-е изд. — М.: Айрис-пресс, 2008.
• И. А. Марон. Дифференциальное и интегральное исчисление в примерах и задачах (Функции одной переменной).
  4 стр., 1640 слов

  Курсовик — Анализ исполнения доходной части бюджета Санкт-Петербурга ...

  ... Федерации. Региональные бюджеты - составная часть финансовой системы Российской Федерации. К региональным бюджетам относятся бюджеты 21 республики в составе Российской Федерации, 55 краев, областей и городов Москвы и Санкт-Петербурга, бюджеты 10 ...

  — М., Физматлит, 1970.

• В. Д. Черненко. Высшая математика в примерах и задачах: Учебное пособие для вузов. В 3 т. — СПб.: Политехника, 2003.

4.2.4.2.5. Справочники

• Таблица производных
• Список интегралов

4.2.5.3. Классические произведения

• Лопиталь. Анализ бесконечно малых
• Bernulli, Johann. Die erste Integrelrechnunug/Leipzig-Berlin, 1914.
• Эйлер. Введение в анализ, Дифференциальное исчисление, Интегральное исчисление
• Коши. Краткое изложение уроков по дифференциальному и интегральному исчислению
• Штурм. Курс анализа. Т.1,2 — Классический курс парижской политехнической школы 1830-х годов.
• Гурса Э. Курс мат. анализа. T. 1.1, 1.2
• М. Е. Ващенко-Захарченко, Алгебраический Анализ или Высшая Алгебра, 1887. — Первый российский учебник по мат. анализу.

4.3.4. Сочинения по истории анализа

• Кестнер, Авраам Готтгельф. Geschichte der Mathematik. 4 тома, Геттинген, 1796—1800
• Кантор, Мориц. Vorlesungen über geschichte der mathematik Leipzig: B. G. Teubner, 1894—1908. Bd. 1, Bd. 2, Bd. 3, Bd. 4
• История математики под редакцией А. П. Юшкевича (в трёх томах):

• Том 1 С древнейших времен до начала Нового времени. (1970)
• Том 2 Математика XVII столетия. (1970)
• Том 3 Математика XVIII столетия. (1972)

• Маркушевич А. И. Очерки по истории теории аналитических функций. 1951
• Вилейтнер Г. История математики от Декарта до середины XIX столетия. 1960

Примечания

1. Ср., напр.,курс Cornell Un — www.math.cornell.edu/Courses/FSM/firstyearcalc.html
2. Ньютон И. Математические работы . M, 1937.
3. Leibniz //Acta Eroditorum, 1684. L.M.S., т. V, c. 220—226. Рус. пер.: Успехи Мат. Наук, т. 3, в. 1 (23), с. 166—173.
4. Лопиталь. Анализ бесконечно малых . М.-Л.:ГТТИ, 1935. (Далее: Лопиталь) // Мат. анализ на EqWorld — eqworld.ipmnet.ru/ru/library/mathematics/calculus.htm
5. Лопиталь, гл. 1, опр. 2.
6. Лопиталь, гл. 4, опр. 1.
7. Лопиталь, гл. 1, требование 1.
8. Лопиталь, гл. 1, требование 2.
9. Лопиталь, гл. 2, опр.
10. ↑ ^{1 2} Лопиталь, § 46.
11. Лопиталь беспокоится о другом: dy для него длина отрезка и нужно пояснить, что значит её отрицательность. Замечание, сделанное в § 8-10, можно даже понять так, что при убывании y с ростом x следует писать dxy = ydx − xdy , однако далее это не используется.
12. Bernulli, Johann. Die erste Integrelrechnunug. — historical.library.cornell.edu/cgi-bin/cul.math/docviewer?did=Bern002&view=50&frames=0&seq=7 Leipzig-Berlin, 1914.
13. См.: Успехи Мат. Наук, т. 3, в. 1 (23)
14. См. Маркушевич А. И. Элементы теории аналитических функций , Учпедгиз, 1944. С. 21 и сл.; Koenig F. Kommentierender Anhang zu Funktionentheorie von F. Klein . Leipzig: Teubner, 1987; а также Исторический очерк в статье Функция
15. Эйлер. Введение в анализ . Т. 1. Гл. 1, § 4
16. Эйлер. Введение в анализ . Т. 1. Гл. 1, § 6
17. Эйлер обозначает это число как i , что не может не путать современного читателя.
18. Введении в анализ , т. 1, гл. 8
19. Некоторые исследователи (см., напр., История Математики, т. 2) хотят видеть в сказанном во втором томе Введения в анализ ростки новой трактовки понятия функции, но в тексте говорится лишь о том, что кривые, а вовсе не функции, могут не быть представимы в виде единого выражения для счёта, то есть одной функции.
20. Casorati F. Teorica delle funzioni di variabili complesse . Pavia, 1868. P. 191
21. Эйлер. Интегральное исчисление . Т. 1, опр. 2
22. Lagrange. OEvres . Vol. 9 — gdz.sub.uni-goettingen.de/no_cache/en/dms/load/toc/?IDDOC=41270
23. Lacroix. Traite du calcul differentiel et du calcul integral . Vol. 1-3. 1 ed., 1798. (Большой Лакруа)// http://gallica.bnf.fr — gallica.bnf.fr
24. См. также: Маркушевич А. И. Элементы теории аналитических функций . М., 1944. C. 22-24
25. Lacroix. Traite , vol. 2, § 594.
26. См. также: История математики , т. 3., с. 297—300
27. Pringssheim A.// Math. Ann. Bd. 43 (1893); см. также: Маркушевич А. И. Элементы теории аналитических функций . М., 1944. C. 16-17.

Данный реферат составлен на основе .

Динамика валютного курса рубля и ее роль в экономике России

... оказывает на экономический рост и какова величина этого роста - не полный список тем, обсуждаемых в средствах массовой информации. Целью курсовой работы является изучение валютного курса и его влияния ... Для учета влияния на валютный курс уровня инфляции в стране котировки и в иностранном государстве определяют реальный курс. Реальный курс - это номинальный валютный курс, пересчитанный с учетом ...