Математические методы в экономике

метки: Переменный, Модель, Экономический, Теория, Задача, Клетка, Программирование, Строка

Исторически математическая экономика началась с моделей простого и расширенного воспроизводства. В них отражались потоки денег и потоки товаров и продуктов. Это, например, модель Ф. Кенэ. Позднее эти модели подробно и более глубоко изучались в экономической кибернетике — здесь можно указать на работы О. Ланге. Рассмотрены схемы денежных и материальных потоков, обеспечивающих простое и расширенное воспроизводство, их идентификацию, модели математической статистики. Далее возникли концепции производственных функций, предельных и маргинальных значений, предельных полезностей и субъективных полезностей. Дальнейшее развитие — в рамках линейного и выпуклого программирования, выпуклого анализа.

Далее: развитие тонких техник моделирования: имитационное моделирование, экспертные системы, нейронные сети.

Понятие субъективной полезности ввел в 18-ом веке Ф.Галиани. Затем это понятие и понятие предельной полезности развивали с середины 19-ого века: в рамках австрийской школы — К.Менгер, В.Бем-Баверк, Ф.Визер.

Эти же понятия, а также углубленное развитие модели экономического равновесия — в рамках математической школы: Л.Вальрас, У.Джевонс, Эджворт.

И австрийская, и математическая школы связаны с маржиналистской концепцией. Точный вид маргинальные оценки получили в теории двойственности в математическом программировании.

Исследование операций в экономике – это научная дисциплина, целью которой является количественное обоснование принимаемых решений. С помощью специальных математических методов решается определенный класс экономических задач. К таким задачам относятся:

• задача об оптимальном использовании ограниченных ресурсов (сырьевых, трудовых, временных);
• задача сетевого планирования и управления;
• задачи массового обслуживания;
• задачи составления расписания (календарного планирования);
• задачи выбора маршрута и другие.

Оптимизационная задача, в которой целевая функция и неравенства (уравнения), входящие в систему ограничений являются линейными функциями, называется задачей линейного программирования.

Общая задача линейного программирования имеет вид:

(1.1) (1.2)

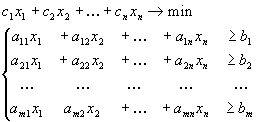
(1.3)

Функция (1.1) называется целевой функцией. Система (1.2) называется системой ограничений, а условие (1.3) – условием неотрицательности.

§1. «Геометрическая интерпретация ЗЛП. Графический метод решения ЗЛП»

Графический метод решения ЗЛП основан на следующих утверждениях.

Система ограничений ЗЛП геометрически представляет собой выпуклый многоугольник или выпуклую многоугольную область как пересечение полуплоскостей — геометрических образов неравенств системы.

Целевая функция Z = c ₁ x₁ + c₂ x₂ геометрически изображает семейство параллельных прямых, перпендикулярных вектору нормали N(с₁ ,с₂ ).

Эти прямые называются линиями уровня.

Линия уровня – это прямая, вдоль которой целевая функция принимает фиксированное значение.

Теорема. При перемещении линии уровня в направлении вектора нормали N значение целевой функции возрастает, в противоположном направлении — убывает.

Алгоритм графического метода решения ЗЛП.

1. В системе координат построить прямые по уравнениям, соответствующим каждому неравенству системы ограничений;

2. найти полуплоскость решения каждого неравенства системы (обозначить стрелками).

Для определения полуплоскости необходимо выбрать любую контрольную точку, не лежащую на данной прямой. Подставить ее координаты в систему ограничений. Если неравенство выполняется, то нужно выбрать полуплоскость, содержащую контрольную точку. Если неравенство не выполняется нужно выбрать полуплоскость, не содержащую контрольную точку. В качестве контрольной точки рекомендуется выбирать точку с координатами (0;0);

3. найти многоугольник (многоугольную область) решений системы ограничений как пересечение полуплоскостей;

4. построить вектор нормали N. Начало вектора нормали в точке с координатами (0;0), конец вектора в точке с координатами (с ₁ , с₂ );

5. через начало координат построить линию уровня, перпендикулярно к вектору нормали;

6. перемещать линию уровня параллельно самой себе по области решения в угловые точки, достигая max f при движении вектора N (min f при движении в противоположном направлении);

7. найти координаты точки max (min).

Для этого необходимо решить систему уравнений прямых, которые пересекаются в этой точке или определить координаты по графику;

8. вычислить значение целевой функции в этой точке (ответ).

§2. «Симплексный метод решения ЗЛП»

Симплексный метод представляет собой схему получения оптимального плана за конечное число шагов.

Для использования симплексного метода ЗЛП должна быть приведена к каноническому виду, т.е. система ограничений должна быть представлена в виде уравнений.

Оптимизационные исследования ЗЛП удобно проводить, пользуясь симплекс-таблицами. Существует достаточно большое количество форм симплекс-таблиц. Воспользуемся одной из форм, по которой рекомендуется следующий порядок решения ЗЛП:

1 . Математическая модель задачи приводится к канонической форме с помощью дополнительных неотрицательных переменных.

2. Определяется начальное базисное допустимое решение. Для этого переменные разбивают на две группы – основные (базисные) и неосновные. В качестве основных переменных следует выбрать (если возможно) переменные, каждая из которых входит только в одно из уравнений системы ограничений. Дополнительные переменные удовлетворяют этому правилу.

3. Составляется исходная симплекс-таблица (таблица 1), в которую записывают параметры, соответствующие начальному базисному допустимому решению:

3.1. Весовые коэффициенты c_j при переменных x_j (j = 1,…,n) целевой функции (строка C ).

3.2. Весовые коэффициенты c_i при базисных переменных x_i (i = 1,…,m) целевой функции (столбец C _b ).

3.3. Переменные x_i (i = 1, … ,m) , которые входят в текущий базис (столбец A_b ).

3.4. Свободные коэффициенты b_i (i =1, … ,m) уравнений ограничений (столбец B).

В этом же столбце находим оптимальный план задачи.

3.5. Элементы a _ij (i = 1, … ,m ; j = 1, … ,n) матрицы условий задачи (столбцы A₁ , .., A_n ).

Таблица 1

А б	С б	В	c 1	…	c j	…	c k	…	c n
			A 1	..	A j	..	A k	..	A n
А 1	c 1	b 1	a 11	..	a 1j	..	a 1k	..	a 1n
…	..	..	..	..	..	..	..	..	..
А i	c i	b i	a i1	..	a ij	..	a ik	..	a in
…	..	..	..	..	..	..	..	..	..
A r	c r	b r	a r1	..	a rj	..	a rk	..	a rn
…	..	..	..	..	..	..	..	..	..
A m	c m	b m	a m1	..	a mj	..	a mk	..	a mn
m+1	S	S 1	..	S j	..	S k	..	S n

3.6. Оценки S_j (j=1, … ,n) векторов условий A_j , которые определяются по формуле:

где c _i — весовые коэффициенты при базисных переменных.

_j

• если S _j ³ 0 для всех j = 1, …, n, то полученное решение является оптимальным;

• если имеются S _j <
• 0 и в столбцах A_j , соответствующих этим отрицательным оценкам, существует хотя бы один элемент a_ij >
• 0, то возможен переход к новому решению, связанному с большим значением целевой функции;

• Из отрицательных оценок выбирают ту, у которой значение по абсолютной величине больше. Если имеется несколько одинаковых отрицательных оценок, то выбирают ту, которой соответствует максимальный коэффициент целевой функции c _i .

• если имеются S _k <0 и в столбце A_k все элементы a_ik £ 0, то в области допустимых решений целевая функция не ограничена сверху.

4. Определяется вектор A_k , который необходимо ввести в базис для улучшения решения, по наибольшему значению S_k . Переменная этого столбца x_k будет новой базисной переменной, которая вводится в базис. Столбец, содержащий эту переменную, называется направляющим столбцом.

5. Определяется вектор, который нужно вывести из базиса, используя равенство:

x _r

6. Заполняется таблица соответствующая новому базисному решению. В этой таблице, прежде всего заполняются клетки строки r с вводимой переменной x_k . Для этого все элементы этой строки делятся на направляющий элемент. Получаются элементы новой строки:

b _r /a_rk , a_r1 /a_rk , … , a_rn /a_rk .

Остальные элементы новой таблицы определяются по правилу прямоугольника:

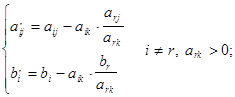Процесс вычислений заканчивается, когда найдено оптимальное решение см. п.п.3.6.

Критерий оптимальности решения для нахождения максимального значения целевой функции: если в выражении линейной функции через неосновные переменные отсутствуют положительные коэффициенты при неосновных переменных, то решение оптимально.

Критерий оптимальности решения для нахождения минимального значения целевой функции: если в выражении линейной функции через неосновные переменные отсутствуют отрицательные коэффициенты при неосновных переменных, то решение оптимально.

§3. «Метод искусственного базиса».

Если ограничения исходной задачи содержат единичную матрицу порядка М, то при неотрицательности правых частей уравнений определен первоначальный план, из которого с помощью симплекс – таблиц находится оптимальный план.

Если ограничения можно привести к виду:

Ах≤А ₀ при А₀ ≥0, то система ограничений содержит единичную матрицу всегда.

Если задача не содержит единичной матрицы и не приводится к указанному виду, то для решения задачи используется метод искусственного базиса.

Для получения единичной матрицы к каждому ограничению прибавляют по одной неотрицательной переменной, которые называются искусственными. Единичные вектора, соответствующие искусственным переменным, образуют искусственный базис.

В целевую функцию искусственные переменные добавляются с коэффициентом М, если задана задача на нахождение минимума. В этом случае величина М предполагается достаточно большим положительным числом. Если необходимо найти минимальное значение целевой функции, то искусственные переменные записывают с коэффициентом (-М), который предполагается достаточно малым отрицательным числом. Для нахождения оптимального плана в случае, если заранее не задана величина М, применяется симплекс-метод, который в таблице имеет на одну строку больше, чем обычная симплекс-таблица.

Строка оценок разбивается на две:

• (m+1) – оценка, не зависящая от М;
• (m+2) – коэффициент при М.

По (m+2) строке определяют вектор, подлежащий включению в базис. Итерационный процесс проводят до исключения из базиса всех искусственных векторов. Затем процесс продолжают по (m+1) строке обычным симплекс-методом.

§4. «Транспортная задача»

Классическая транспортная задача формулируется следующим образом:

_j

Требуется составить такой план перевозок, при котором все заявки пунктов потребления полностью выполнялись бы пунктами отправления, а общая стоимость перевозок была минимальной.

При такой постановке данную задачу называют транспортной задачей по критерию стоимости.

В общем виде исходные данные представлены в таблице 9.

Таблица 9

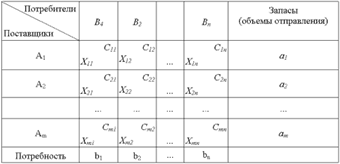
закрытой

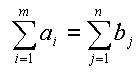
открытой

П.1 Алгоритм метода минимального элемента.

1. Из распределительной таблицы 9 выбирают наименьшую стоимость и в клетку, которая ей соответствует, помещают меньшее из чисел a _i или b_j (если таких клеток несколько, то выбирают любую);

2. Из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и то и другое;

3. Из оставшейся части таблицы снова выбирают наименьшую стоимость и процесс продолжается до тех пор, пока все запасы не будут вывезены, а потребности удовлетворены;

4. Рассчитывают транспортные расходы: сумма произведений количества перевезенной продукции на стоимость для занятых клеток.

П. 2 Алгоритм метода Фогеля.

1. В каждой строке находят разность между двумя наименьшими стоимостями и записывают ее около соответствующей строки справа;

2. В каждом столбце находят разность между двумя наименьшими стоимостями и записывают ее под соответствующим столбцом;

3. Среди всех полученных разностей находят максимальную и распределяют объем перевозки в клетку строки или столбца с наименьшей стоимостью;

4. Исключают из рассмотрения строку или столбец с распределенными поставками и возвращаются к пункту 1. Процесс продолжается до тех пор, пока все запасы не будут вывезены, а потребности удовлетворены;

5. Когда план построен, рассчитываются транспортные расходы.

1. В таблице 9 в каждом столбце отмечают галочкой клетку с наименьшей стоимостью и в каждой строке отмечают галочкой клетку с наименьшей стоимостью;

2. В клетки с двумя галочками записывают максимально возможные объемы перевозок, каждый раз, исключая соответствующий столбец или строку;

3. Распределяют перевозки по клеткам с одной галочкой;

4. В оставшейся части таблицы перевозки распределяют в клетки с наименьшей стоимостью.

5. Когда план построен, рассчитываются транспортные расходы.

П.4. Алгоритм метода северо-западного угла.

1. Пользуясь таблицей 9 распределяют груз, начиная с левой верхней, условно называемой северо-западной, клетки (1,1).

Необходимо удовлетворить потребности В ₁ за счет поставщика А₁ ;

2. а).

Если b ₁ >a₁ , в клетку (1,1) записывают a₁ и строку 1 вычеркивают из рассмотрения;

b).

Если a ₁ >b₁ , в клетку (1,1) записывают b₁ и столбец 1 вычеркивают из рассмотрения;

3. а).

Если b ₁ >a₁ , ∆= b₁ — a₁ – неудовлетворенные потребности. Спускаются на клетку вниз и сравнивают ∆ с a₂ ;

b).

Если a ₁ >b₁ , ∆=a₁ — b₁ – не вывезенные запасы. Двигаются по строке вправо и сравнивают ∆ с b₂ ;

4. Необходимо вернуться к пункту 2;

5. Рассчитываются транспортные расходы.

П.5. Алгоритм метода потенциалов.

1. проверяется тип модели транспортной задачи и в случае открытой модели сводим ее к закрытой;

2. находится опорный план перевозок путем составления 1-й таблицы одним из способов — северо-западного угла или наименьшей стоимости;

3. проверяем план (таблицу) на удовлетворение системе уравнений и на невыражденность; в случае вырождения плана добавляем условно заполненные клетки с помощью « 0 »;

4. для опорного плана определяются потенциалы u _i и v_j , соответствующие базисным клеткам, по условию:

u _i + v_j = c_ij

Таких уравнений будет m + n — 1 , а переменных будет m + n. Для их определения одну из переменных полагают равной любому постоянному значению. Обычно принимают u ₁ = 0.

После этого для небазисных клеток опорного плана определяются оценки ,

где

При этом если £0, то опорный план оптимален, если же среди окажется хотя бы один положительный элемент, то опорный план можно улучшить.

Улучшение опорного плана осуществляется путем целенаправленного переноса из клетки в клетку транспортной таблицы отдельных перевозок без нарушения баланса по некоторому замкнутому циклу.

Циклом транспортной таблицы называется последовательное соединение замкнутой ломаной линией некоторых клеток, расположенных в одном ряду (строке, столбце), причем число клеток в одном ряду должно быть равно двум.

Каждый цикл имеет четное число вершин, одна из которых в клетке с небазисной переменной, другие вершины в клетках с базисными переменными. Клетки отмечаются знаком «+», если перевозки в данной клетке увеличиваются и знаком «–» в противном случае. Цикл начинается и заканчивается на выбранной небазисной переменной и отмечается знаком «+». Далее знаки чередуются.

Количество единиц продукта, перемещаемого из клетки в клетку по циклу, постоянно, поэтому сумма перевозок в каждой строке и в каждом столбце остаются неизменными. Стоимость всего плана изменяется на цену цикла.

Цена цикла

Улучшение опорного плана осуществляется путем нахождения цикла с отрицательной ценой.

5. Если критерий оптимальности не выполняется, то переходим к следующему шагу. Для этого:

а) в качестве начальной небазисной переменной принимается та, у которой оценка имеет максимальное значение;

• б) составляется цикл пересчета;

в) находится число перерасчета по циклу: число X=min{X _ij }, где X_ij — числа в заполненных клетках со знаком « — »;

• г) составляется новая таблица, добавляя X в плюсовые клетки и отнимая X из минусовых клеток цикла;

6. Возвращаются к пункту 3 и т.д.

7. Через конечное число шагов (циклов) обязательно приходят к ответу, так как транспортная задача всегда имеет решение.

§5. «Задачи целочисленного программирования. Метод Гомори»

Задача линейного целочисленного программирования формулируется следующим образом:

Найти такое решение (план) Х=(х ₁ , х₂ ,…, х_n ), при котором линейная функция

(5.1)

(5.2) (5.3) (5.4)

принимает максимальное значение при ограничениях:

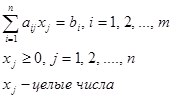
Методы целочисленной оптимизации можно разделить на три основные группы:

• a. методы отсечения;
• b. комбинаторные методы;
• c. приближенные методы.

Подробнее остановимся на методах отсечения. Сущность методов отсечения состоит в том, что сначала задача решается без условий целочисленности. Если полученный план целочисленный, задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:

• оно должно быть линейным;
• должно отсекать найденный оптимальный нецелочисленный план;
• не должно отсекать ни одного целочисленного плана.

Дополнительное ограничение, обладающее указанными свойствами, называется правильным отсечением.

Далее задача решается с учетом нового ограничения. После этого в случае необходимости добавляется еще одно ограничение и т.д.

Один из алгоритмов решения задачи линейного целочисленного программирования, предложенный Гомори, основан на симплексном методе и использует достаточно простой способ построения правильного отсечения.

Алгоритм метода Гомори:

1. Симплексным методом решается задача (5.1)-(5.3) без учета условия целочисленности. Если все компоненты оптимального плана целые, то он является оптимальным и для задачи целочисленного программирования (5.1)-(5.4).

Если первая задача (8.1)-(8.3) неразрешима (т.е. не имеет конечного оптимума или условия ее противоречивы), то и вторая задача (5.1)-(5.4) также неразрешима.

2. Если среди компонент оптимального решения есть нецелые, то выбирают компоненту с наибольшей целой частью и по соответствующему уравнению системы ограничений формируется правильное отсечение:

(5.5)

3. Неравенство (5.5) введением дополнительной неотрицательной целочисленной переменной преобразовывают в равносильное уравнение

(5.6)

и включить его в систему ограничений (5.2).

4. Полученную расширенную задачу решить симплексным методом. Если найденный оптимальный план будет целочисленным, то задача целочисленного программирования (5.1)-(5.4) решена. В противном случае возвратиться к пункту 2.

Если задача разрешима в целых числах, то после конечного числа шагов (итераций) оптимальный целочисленный план будет найден.

Заключение.

Задачи экономической науки, требующие применения математики

Имеется ряд определений предмета экономической теории. Из них вытекает необходимость экономико-математических методов, причем требуется самая изощренная современная математика, как теоретическая, так и прикладная. Фактически существует такая дисциплина, как математическая экономика, которая у ряда авторов представляет собой чисто математическую теорию с типичным для нее построением: формальные определения с соответствующими примерами реальных объектов, затем теоремы, их точные доказательства, интерпретация этих теорем. Такой способ построения экономической теории напоминает о некоторых реализациях такой дисциплины, как математическая физика, в виде чисто математической абстрактной теории. Все это крайности, которые необходимы для интенсивного развития математического аппарата, но они должны быть лишь частью теории, служащей некоторым содержательным, жизненно необходимым и в конечном счеты неформализуемым задачам.

Определения экономической теории, синтезированные из работ ряда авторов (таких, как Э.Маленво, П.Самуэльсон, Г.Саймон, И.Экланд):

Экономическая теория — это наука, которая:

Во-первых, изучает проблемы наилучшего использования ограниченных возможностей человеческой деятельности.

Но так как люди редко действуют рационально и эффективно, то:

Во-вторых, она изучает РЕАЛЬНОЕ поведение человека, который В ПРИНЦИПЕ умеет связывать экономические цели и средства их достижения.

Дальше идёт конкретизация:

В-третьих, она изучает, как ограниченные ресурсы используются для удовлетворения потребностей людей, живущих в обществе. И потому предмет её исследований — это основные экономические процессы, такие, как производство, распределение благ и их потребление. С другой стороны, экономическая теория изучает институциональные структуры и процессы, преследующие цель организации упорядоченного прохождения этих операций и процессов.

В-четвёртых, экономическая теория описывает и изучает человеческий выбор, в том числе — обмен в условиях ограничений. Ограниченные ресурсы, которые здесь существенны — это материальные, трудовые, финансовые, технологические, информационные и другие. Информационная сторона экономических процессов становится все более важной, в связи с чем все большее значение приобретает экономическая информатика.

В-пятых, теория изучает, как из индивидуальных способов поведения, рассматриваемых, как исходные, как заданные, выводятся закономерности на уровне общества; как индивидуальные решения синтезируются в коллективные.

При этом следует сказать, что экономическая теория может быть как дескриптивной, так и нормативной.

Дескриптивная — описательная — экономическая теория описывает поведение людей при выборе экономических действий (на основе оценок текущего состояния, его диагностики и прогнозирования его развития).

Нормативная теория даёт рекомендации по оптимальному экономическому поведению.

Таким образом, в абстрактной форме основные задачи экономики суть математические задачи выбора и диагностики (сюда включаются и прогнозирование, и оценки ситуаций), усложнённые неформализованными элементами, противоречивыми, сингулярными моделями и т.д.

Математика в экономической науке, в экономической информатике применяется во все больших масштабах. Сейчас очевидно, что она — необходимая часть экономической теории. Однако она недостаточна, так как и чисто экономическая содержательная составляющая становится все более сложной, а неформализованная сторона описания экономических явлений всегда будет присутствовать.

И существует не только рациональный выбор индивидуумами их решений, который есть предмет неоклассической экономической теории. Рациональное целесообразное поведение ограничено в своих возможностях — с точки зрения ресурсов, организационных возможностей, степени охвата разнообразных, разноплановых, в том числе и неформализованных, связей, с точки зрения возможности учёта традиций, психологии и так далее.

Оно ограничено также потенциалом вычислительных средств для вычисления эффективного поведения и учёта поведения других субъектов. Это и требует дополнения неклассической теории (основанной на принципах целесообразного поведения) другими средствами моделирования. Неоклассическая теория базируется на концепции выбора из множества альтернатив с использованием функции полезности.

Но это нужно дополнить средствами решения таких проблем:

1. как обнаруживать и записывать эти альтернативы, их множество и способы выбора из них;

2. как описывать и идентифицировать функцию полезности или отношения предпочтения;

3. Как связывать альтернативы, полезности, действия, выбора и реализации альтернатив (причем и чисто эмпирические реализации);

4. как учитывать реальную и нормативную рациональную эмпирику;

5. как учитывать ограничения на передачу информации (скорость, объемы) и на вычислительную сложность.

В отношении экономики можно сказать, что это динамическая система — множество, обладающее целостностью, в котором эволюционируют и элементы множества, и их свойства, и отношения между ними.

Систему, в том числе алгебраическую, можно рассматривать и как инструмент принятия решений, и как модель, как способ восприятия реальных феноменов.

Абстрактная система — это совокупность взаимосвязанных переменных (разной алгебраической природы), отражающих характеристики описываемого явления или объекта. Фактически это математическая модель. Опишем структуру системы. В систему входят:

• совокупность взаимосвязанных элементов;
• субъект исследования — исследователь;
• формулировка задачи — отношения наблюдателя, исследователя, к совокупности элементов, соответствующий отбор элементов и их существенных свойств;
• отношения между элементами;
• описание наборов элементов, переменных, параметров и констант, а также связей между ними.

И теперь нужно обратиться к понятию структуализма в экономической теории. Структуралистская идея заключается в аксиоматическом формальном задании отношений и связей между элементами системы, включая как идентифицированные, так и неизвестные элементы, первоначально заданные чисто символически. Кроме того задается логика анализа следствий из имеющихся посылок и правил вывода. В результате многократного применения (иногда в бесконечном процессе) этих правил происходит частичная или полная идентификация искомых блоков модели.

Структурное исследование экономики — это:

• логико-математическое описание реальных или абстрактных процессов и явлений;

— если же имеет место дополнение постструктуалистской методологией, то к этому добавляется подобное изучение во всей многоплановости и полноте экономических явлений, в их противоречивости и возможной неформализованности.

Модели математической экономики

Математическая экономика изучает свойства экономической динамики и равновесия с помощью математических моделей этих феноменов и точного исследования моделей. При этом получены условия положительного экономического роста и условия равновесия экономики при различных предположениях о природе производства. и распределения продуктов, о механизме рынка и установления цен, ренты и других экономических величин.

Классические модели математической экономики таковы:

• модель оптимального использования ограниченных ресурсов в технологических способах. Это модель оптимального выбора;
• модель Леонтьева — модель межотраслевого баланса — как в статической, так и в динамической формах. Это модель прямых, косвенных и полных взаимосвязей подразделений экономики;
• теоретико-игровые модели;
• модель фон Неймана о росте капитала и натурального производства, об образовании ценностей товаров и о вычислении объективно обоснованной ренты;
• модели технологических множеств и теоремы о магистралях как образцовых траекториях экономического развития;
• модели равновесия: Вальраса, Эрроу, Дебре и других;
• модели обмена, в том числе международного;
• модели согласования предпочтений экономических субъектов;
• модели прямого и расширенного воспроизводства национальной экономики;
• В настоящее время интенсивно развиваются модели финансовой и актуарной математики, которые включают в себя в качестве блоков математическую статистику и распознавание образов.

Модели исследования операций являются граничащими с математической экономикой моделями, они дополняют теоретические исследования и позволяют строить и исследовать более практические модели — такие, например, как модели управления запасами, модели календарного планирования и другие.

Используемая литература:

1. Е.С. Вентцель. Исследование операций: задачи, принципы, методология. — М.: 2004.

2. О.А. Косоруков, А.В. Мищенко. Учебник для ВУЗов. — М.: «Экзамен», 2003.

3. Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман.- М.: ЮНИТИ, 2002.

4. Хемди А. Таха. Введение в исследование операций. 6-е издание: пер. с англ.-М.: Издательский дом «Вильямс», 2001.

5. П.В. Конюховский. Математические методы исследования операций. — М.: Питер, 2000.

6. Н.Ш. Кремер. Исследование операций в экономике. — М.: «Банки и биржи» Издательское объединение «ЮНИТИ», 1997.

7. А. Б. Аронович, М.Ю.Афанасьев, Б.П. Суворов. Сборник задач по исследованию операций. – М.: Издательство МГУ, 1997.

8. Ю.И. Дегтярев. Системный анализ и исследование операций. Учебник для ВУЗов. – М.: Высшая школа, 1996.

9. Г. Вагнер. Основы исследований операций. Т.1-3. — М.: Мир, 1972.

10. Исследование операций. Учебник для ВУЗов под общей редакцией д.э.н. Н.П. Тихомирова.