Нелинейные математические модели в системах компьютерной математики

метки: Математический, Модель, Решение, Программирование, Оптимальный, Исследование, Задача, Логистический

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМЕНИ М.Е. ЕВСЕВЬЕВА»

Факультет физико–математический, Кафедра информатики и вычислительной техники, Реферат на тему:

Нелинейные математические модели в системах компьютерной математики

Выполнила: Захаркина Р.А.

Студентка 3 курса группы МДМ -215

Проверила: кан. физ-мат. наук, доцент

Кормилицына Т.В

Саранск 2017

1. Понятие операционного исследования

Bпервые математические модели были использованы для решения практической задачи в 30-х годах в Великобритании при создании системы противовоздушной обороны. Для разработки данной системы были привлечены ученые различных специальностей. Система создавалась в условиях неопределенности относительно возможных действий противника, поэтому исследования проводились на адекватных математических моделях. В это время впервые был применен термин: «операционное исследование», подразумевающий исследования военной операции. В последующие годы операционные исследования или исследования операций развиваются как наука, результаты которой применяются для выбора оптимальных решений при управлении реальными процессами и системами.

Решения человек принимал всегда и во всех сферах своей деятельности. Раньше хотели, чтобы принимаемые решения всегда были правильными. Теперь принято говорить, что решения должны быть оптимальными. Чем сложнее объект управления, тем труднее принять решение, и, следовательно, тем легче допустить ошибку. Вопросам принятия решений на основе применения ЭВМ и математических моделей посвящена новая наука «Исследование операций», приобретающая в последние годы все более обширное поле приложений. Эта наука сравнительно молодая, ее границы и содержание нельзя считать четко определенными.

Предмет под названием «Исследование операций» входит в программу элитарных вузов, но не всегда в этот термин вкладывается одно и то же содержание. Некоторые ученые под «исследованием операций» понимают, главным образом, математические методы оптимизации, такие как линейные, нелинейные, динамическое программирование. Другие к исследованию операций подходят с позиции теории игр и статистических решений. Наконец, некоторые ученые вкладывают в понятие «исследование операций» чрезмерно широкий смысл, считая ее основой системного анализа и «наукой наук».

Система электронных расчетов. Учет операций по электронным платежам

... что только широкое внедрение электронной системы безналичных денежных расчетов способно поднять экономику ... денежных знаков; это денежные расчеты путем записей по счетам в банках. Деньги при этом списываются со счета плательщика и зачисляются на счет получателя. Операции по безналичным расчетам ... системы. Результатом этой работы был план Центрального Банка России “Стратегия развития платежной системы ...

Под термином «исследование операций» мы будем понимать применение математических, количественных методов для обоснования решений во всех областях целенаправленной человеческой деятельности.

Окончательно термин «исследование операций» закрепился в конце Второй мировой войны, когда в вооруженных силах США были сформированы специальные группы математиков и программистов, в задачу которых входила подготовка решений для командующих боевыми действиями. В дальнейшем исследование операций расширило область своих применений на самые разные области практики: экономика, транспорт, связь и даже охрана природы.

Чтобы человеку принять решение без ЭВМ, зачастую ничего не надо, кроме опыта и интуиции. Правда, никакой гарантии правильности, а тем более оптимальности при этом нет. Подчеркнем, что ЭВМ никаких решений не принимает. Решение принимает человек (ЛПР).

А ЭВМ только помогает найти варианты решений. Непременное присутствие человека (как окончательный инстанции принятия решений) не отменяется даже при наличии полностью автоматизированной системы управления. Нельзя забывать о том, что само создание управляющего алгоритма, выбор одного из возможных его вариантов, есть тоже решение. По мере автоматизации управления функции человека перемещаются с одного уровня управления на другой — высший. Основные этапы решения задачи принятия оптимальных решений с помощью ЭВМ показаны на Рис. 1.

Исходные

данные



Объект



Задача



Модель



Алгоритм



Программа



ЭВМ



Пакет прикладных программ (ППП)



Решение

Рис. 1. Основные этапы решения задачи принятия решения с помощью ЭВМ.

Выбор задачи — важнейший вопрос. Какие основные требования должна удовлетворять задача? Таких требований два:

должно существовать, как минимум, два варианта ее решения (ведь если вариант один, значит и выбирать не из чего);

надо четко знать в каком смысле искомое решение должно быть наилучшим (кто не знает, куда ему плыть — тому нет и попутного ветра).

Выбор задачи завершается ее содержательной постановкой. Когда производится содержательная постановка задачи, к ней привлекаются специалисты в предметной области. Они прекрасно знают свой конкретный предмет, но не всегда представляют, что требуется для формализации задачи и представления ее в виде математической модели.

Хорошую модель составить не просто. Известный математик Р.Беллман сказал так: «Если мы попытаемся включить в нашу модель слишком много черт действительности, то захлебнемся в сложных уравнениях; если слишком упростим ее, то она перестанет удовлетворять нашим требованиям». Таким образом, исследователь должен пройти между западнями Переупрощения и болотом Переусложнения. Для выполнения успеха моделирования надо выполнить три правила, которые, по мнению древних, являются признаками мудрости. Эти правила применительно к задачам математического моделирования и формулируются так: учесть главные свойства моделируемого объекта; пренебрегать его второстепенными свойствами; уметь отделить главные свойства от второстепенных.

Задача: Решение задач по налогам и налогообложению и ответы на тест

... налог на доходы физических лиц; б) земельный налог; в) транспортный налог; г) акцизы. Какой налог является местным? а) налог на добычу полезных ископаемых; б) налог на добавленную стоимость; в) налог на имущество физических лиц; (К местным налогам относятся: земельный налог; налог на имущество физических лиц; налог на рекламу; налог на ...

Составление модели — это искусство, творчество. Древние говорили: «Если двое смотрят на одно и то же, это не означает, что оба видят одно и то же». И слова древних греков: «Если двое делают одно и то же, это не значит, что получится одно и то же». Эти слова в полной мере относятся к составлению математических моделей. Если математическая модель — это диагноз заболевания, то алгоритм — это метод лечения.

Можно выделить следующие основные этапы операционного исследования:

наблюдение явления и сбор исходных данных;

• постановка задачи;
• построение математической модели;
• расчет модели;

тестирование модели и анализ выходных данных. Если полученные результаты не удовлетворяют исследователя, то следует либо вернуться на этап 3, т.e. предложить для решения задачи другую математическую модель; либо вернуться на этап 2, т.e. поставить задачу более корректно;

применение результатов исследований.

Таким образом, операционное исследование является итерационным процессом, каждый следующий шаг которого приближает исследователя к решению стоящей перед ним проблемы. В центре операционного исследования находятся построение и расчет математической модели.

Математическая модель — это система математических соотношений, приближенно, в абстрактной форме описывающих изучаемый процесс или систему.

Экономико-математическая модель — это математическая модель, предназначенная для исследования экономической проблемы.

Проведение операционного исследования, построение и расчет математической модели позволяют проанализировать ситуацию и выбрать оптимальные решения по управлению ею или обосновать предложенные решения. Применение математических моделей необходимо в тех случаях, когда проблема сложна, зависит от большого числа факторов, по-разному влияющих на ее решение.

Использование математических моделей позволяет осуществить предварительный выбор оптимальных или близких к ним вариантов решений по определенным критериям. Они научно обоснованы, и лицо, принимающее решение, может руководствоваться ими при выборе окончательного решения. Следует понимать, что не существует решений, оптимальных «вообще». Любое решение, полученное при расчете математической модели, оптимально по одному или нескольким критериям, предложенным постановщиком задачи и исследователем.

В настоящее время математические модели применяются для анализа, прогнозирования и выбора оптимальных решений в различных областях экономики. Это планирование и оперативное управление производством, управление трудовыми ресурсами, управление запасами, распределение ресурсов, планировка и размещение объектов, руководство проектом, распределение инвестиций и т.п.

Применение эконометрики в экономическом анализе. Оценка качества моделей

... импорта, оценка эластичности импорта по цене, анализ влияния акциза на предложение и эластичность. Задача работы состоит в использовании аппарата эконометрики в построении и анализе моделей. Математические модели, используемые ... отбора переменных. Ни одна из этих процедур не гарантирует получения оптимального набора переменных. Однако при практическом применении они позволяют получать достаточно ...

2.Классификация математических моделей

Существуют всевозможные классификации математических моделей. Выделяют линейные и нелинейные модели, стационарные и динамические,

модели, описываемые алгебраическими, интегральными и дифференциальными уравнениями, уравнениями в частных производных. Можно выделять классы детерминируемых моделей, вся информация в которых является полностью определяемой, и стохастических моделей, то есть зависящих от случайных величин и функций. Так же математические модели различают по применению к различным отраслям науки. Рассмотрим следующую классификацию математических моделей. Все математические модели разобьем условно на четыре группы.

I. Модели прогноза или расчетные модели без управления. Их можно разделить на стационарные и динамические. Основное назначение этих моделей: зная начальное состояние и информацию о поведение на границе, дать прогноз о поведении системы во времени и в пространстве. Такие модели могут быть и стохастическими. Как правило, модели прогнозирования описываются алгебраическими, трансцендентными, дифференциальными, интегральными, интегро-дифференциальными уравнениями и неравенствами. Примерами могут служить модели распределения тепла, электрического поля, химической кинетики, гидродинамики.

II. Оптимизационные модели. Их так же разбивают на стационарные и динамические. Стационарные модели используются на уровне проектирования различных технологических систем. Динамические – как на

уровне проектирования, так и, главным образом, для оптимального управления различными процессами – технологическими, экономическими и

др. В задачах оптимизации имеется два направления. К первому относятся детерминированные задачи. Вся входная информация в них является полностью определяемой. Второе направление относится к стохастическим процессам. В этих задачах некоторые параметры носят случайный характер или содержат элемент неопределенности. Многие задачи оптимизации автоматических устройств, например, содержат параметры в виде случайных

помех с некоторыми вероятностными характеристиками.

Методы отыскания экстремума функции многих переменных с различными ограничениями часто называются методами математического программирования. Задачи математического программирования – одни из важных оптимизационных задач.

В математическом программировании выделяются следующие основные разделы:

1) Линейное программирование. Целевая функция линейна, а множество, на котором ищется экстремум целевой функции, задается системой линейных равенств и неравенств.

2) Нелинейное программирование. Целевая функция нелинейная и нелинейные ограничения.

3) Выпуклое программирование. Целевая функция выпуклая и выпуклое множество, на котором решается экстремальная задача.

4) Квадратичное программирование. Целевая функция квадратичная, а ограничения – линейные равенства и неравенства.

5) Многоэкстремальные задачи. Задачи, в которых целевая функция имеет несколько локальных экстремумов. Такие задачи представляются весьма проблемными.

Внутривидовая конкуренция и факторы плотности популяций

... животных с различной жизнеспособностью. Популяция характеризуется такими признаками, как численность, плотность населения, его ... и запасы пищи. Образование сообществ Внутривидовые отношения могут носить многообразный характер: ... Дерево оголяется, и между гусеницами возникает конкуренция из-за пищи (см. фото ... выполняет одну за другой различные задачи в определенной последовательности: сначала уход за ...

6) Целочисленное программирование. В подобных задачах на переменные накладываются условия целочисленности.

Как правило, к задачам математического программирования неприменимы методы классического анализа для отыскания экстремума функции нескольких переменных.

Модели теории оптимального управления – одни из важных в оптимизационных моделях. Математическая теория оптимального управления относится к одной из теорий, имеющих важные практические применения, в основном, для оптимального управления процессами.

Различают три вида математических моделей теории оптимального управления. К первому виду относятся дискретные модели оптимального управления. Традиционно такие модели называют моделями динамического программирования. Широко известен метод динамического программирования Беллмана. Ко второму типу относятся модели, описываемые задачам Коши для систем обыкновенных дифференциальных уравнений. Их часто называют моделями оптимального управления системами с сосредоточенными параметрами. Третий вид моделей описывается краевыми задачами, как для обыкновенных дифференциальных уравнений, так и для уравнений в частных производных. Такие модели называют моделями оптимального управления системами с распределенными параметрами.

III. Кибернетические модели. Этот тип моделей используется для анализа конфликтных ситуаций.

Предполагается, что динамический процесс определяется несколькими субъектами, в распоряжении которых имеется несколько управляющих параметров. С кибернетической системой ассоциируется целая группа субъектов со своими собственными интересами.

IV. Вышеописанные типы моделей не охватывают большого числа различных ситуаций, таких, которые могут быть полностью формализированы. Для изучения таких процессов необходимо включение в математическую модель функционирующего «биологического» звена – человека. В таких ситуациях используется имитационное моделирование, а также методы экспертиз и информационных процедур.

3.О нелинейности математических моделей

линейностью

нелинейных явлений

математических моделей

1) существует «равновесная» численность популяции

2) скорость изменения численности популяции пропорциональна самой численности, умноженной (в отличие от модели Мальтуса) на величину ее отклонения от равновесного значения, т.е.

Член (1 — N/N _p ) в этом уравнении обеспечивает механизм «насыщения» численности — при N < N _p (N > N _p ) скорость роста положительна (отрицательна) и стремится к нулю, если .

Модели корпоративной социальной ответственности

... экономическая концепция ответственности, глобальное корпоративное гражданство, управление заинтересованными сторонами. М.Марревийк в работе «Концепции и определения корпоративной социальной ответственности и корпоративной устойчивости» (КУ) ... и зарубежных авторов. В ходе настоящего исследования рассматриваются модели, представленные в работах А.Керолла, М.Шварца, Н.Налбанда, С.Келаби, П.Хонена, ...

Рис. 1.8.

Представляя уравнение (12) в виде

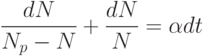
и интегрируя его, получаем

Постоянная интегрирования определяется из условия N(t = 0) = N(0),

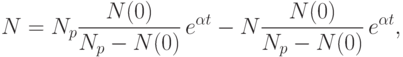
или, в окончательном виде,

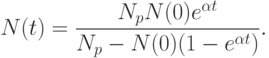
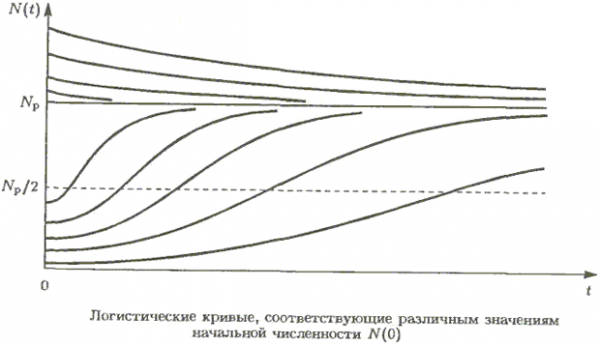
логистической кривой

Логистическая модель более реалистично отражает динамику популяции в сравнении с моделью Мальтуса, но сама она с необходимостью становится нелинейной и поэтому более сложной. Заметим, что предположения о механизмах насыщения используются при построении многих моделей в различных областях знаний.

Реальные процессы, как правило, оказываются линейными в очень ограниченной области. Решение нелинейных уравнений аналитическими методами наталкивается на большие трудности, поэтому они решаются, как правило, численными методами.

Задача 1. Популяционная задача с учетом ограничения по ресурсам

В частности, в модели Мальтуса мы получаем неограниченный рост численности популяции, чего в действительности быть не может – численность, как правило, ограничена наличием тех или иных ресурсов, источников питания и т.п. Эта особенность учтена в так называемой логистической модели, описываемой уравнением

(10)

где — предельная численность популяции, которую может прокормить данная территория

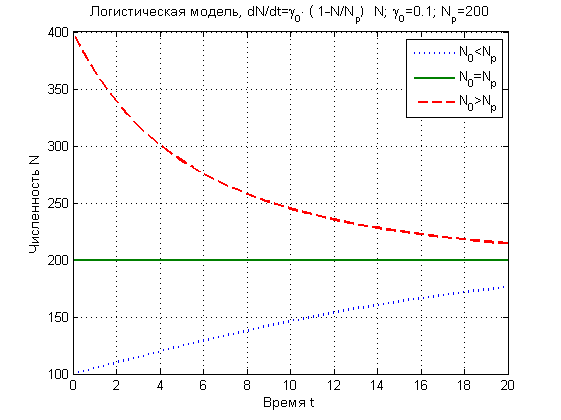
В связи с введением нелинейности решение может иметь различный характер, в частности наблюдаются три различных типа решений:

1. N < Np – идёт экспоненциальный рост, замедляющийся по мере приближения к предельной численности.

2. N = Np – численность не меняется.

3. N > Np — идёт экспоненциальный спад, который замедляется по мере приближения к предельной численности.

Формирование сети мультимодальных транспортно-логистических центров ...

... качеств их развития. Цель исследования: создание теоретической многофакторной модели формирования транспортно-логистических комплексов. Задачи исследования: изучить предпосылки формирования и развития транспортно-логистических комплексов и определить их функционально-организационные характеристики; ...

Рис. 2. Зависимости численности популяции от времени в логистической модели

Проведём моделирование этой задачи в среде

function dn=logistic_model(t,n,gamma,Np)

dn=gamma*(1-n./Np).*n;

Произведём расчёт для трёх различных начальных значений численности, результаты расчёта отобразим на графике (см. рис.2), подпишем оси, вставим заголовок и легенду

[

[

[

plot(t,y,’:’,t1,y1,’-‘,t0,y0,’-.’),

grid, xlabel(‘

title(‘

legend(‘N_0N_p’)

Как видно из рисунка 2, независимо от начальной численности с течением времени количество особей в популяции стремится к предельному значению

Задача 2. Популяционная задача с учетом ограничения по ресурсам и модуляции параметров

Преимуществом численного моделирования является относительная простота, с которой получаются решения для довольно сложных моделей. Например, можно ввести периодическую вариацию параметров задачи. Рассмотрим случай периодической изменчивости коэффициента прироста . Функция, определяющая дифференциальное уравнение, в этом случае записывается

function dn=logistic_model1(t,n,gamma0,Np,T)

gamma=gamma0*(1+cos(2*pi*t/T);

dn=gamma*(1-n./Np).*n;

Результат расчёта для трёх различных начальных состояний при

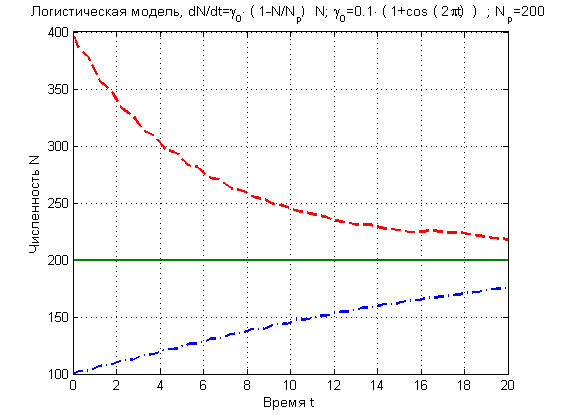
Рис. 3. Зависимости численности популяции от времени в логистической модели с модуляцией коэффициента прироста

Рассмотрим случай периодической изменчивости оптимальной численности популяции . Функция, определяющая дифференциальное уравнение, в этом случае записывается

function dn=logistic_model2(t,n,gamma,Np0,T)

Np=Np0*(1+0.2*cos(2*pi*t/T);

dn=gamma*(1-n./Np).*n;

Как видно из рис.4, во всех решениях, независимо от начального состояния, появляется периодичность. Интересно, что несмотря на симметричность модуляции наблюдается снижение оптимального уровня, происходящее, видимо, за счёт нелинейности задачи.

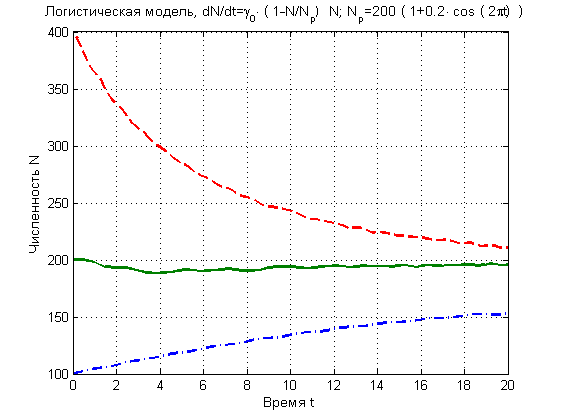
Рис. 4. Зависимости численности популяции от времени в логистической модели с модуляцией оптимального уровня

Инновационное лидерство: моделирование тенденций активности менеджеров ...

... опыта диагностики ресурсов инновационного лидерства менеджеров предприятий, осуществляющих инновационные проекты, и моделированию выявляемых тенденций (по программе психологического инновационного аудита). Инновационное лидерство Р.Л. Дафт связывает ... которых явилась результатом анализа исследований по эволюционной биологии популяций. Эти принципы включают описания развивающихся систем по нескольким ...

Список используемой литературы

1. Бусленко Н.П. Моделирование сложных систем. – М.: Наука, 1978. – 400.

2. Бусленко Н.П. Моделирование сложных систем. – М.: Наука, 1978. – 400.

3. НОУ Интуит [Электронный ресурс] – Режим доступа:

4. Советов Б.Я., Яковлев С.А. Моделирование систем: Практикум. – М.: Высшая школа, 1999. – 224 с.

5. Экштайн В. «Компьютерное моделирование взаимодействия частиц с поверхностью твердого тела.» М. 1995 г.