Финансовые ресурсы, материальную основу которых составляют деньги, имеют временную ценность. Времен ная ценность финансовых ресурсов может рассматривать ся в двух аспектах.
Первый аспект связан с покупательной способностью денег. Денежные средства в данный момент и через опре деленный промежуток времени при равной номинальной стоимости имеют совершенно разную покупательную спо собность. Так. 1000 руб. через какое-то время при уровне инфляции 60% будут иметь покупательную способность всего лишь 400 руб. При современном состоянии экономи ки и уровне инфляции денежные средства, не вложенные в инвестиционную деятельность или на хранение в банк, очень быстро обесцениваются.
Второй аспект связан с обращением денежных средств как капитала и получением доходов от этого оборота. Деньги как можно быстрее должны делать новые деньги.
В любом случае экономист должен уметь определять, сколько будет стоить нынешняя сумма через определенный период, и оценивать будущие доходы сейчас.
Процентными деньгами называют абсолютную величину дохода полученную от предоставления денег в долг.
Процентной ставкой называют относительную величину дохода за оп ределенный период времени.
Периодом наращения называют интервал времени, к которому приуро чена процентная ставка.
Наращением называют процесс увеличения денег, предоставляемых в долг.
Наращенной суммой называют первоначальную сумму вместе с процент ными деньгами.
Множитель наращения показывает во сколько раз наращенная сумма больше первоначальной.
Деньги, кредит и банки
... денег в обращении так называемыми квази деньгами. К квази деньгам относят ликвидные долговые обязательства государства, крупных корпораций и банков: ... денег законам денежного обращения. Инфляция уменьшает завтрашнюю покупательную способность сегодняшних денег, из-за чего накопление в современных деньгах ... продажи в кредит, т.е. с отсрочкой уплаты денег. Характерными признаками функции денег как средства ...
Простыми процентами называют такой способ наращения, при котором проценты начисляются на первоначальную сумму.
Сложными процентами называют такой способ наращения, при котором проценты начисляют на всю накопленную сумку, а не только на первона чальную, как при начислении простых процентов.
Декурсивными процентами называют проценты начисляемые по принципу наращения на сумму долга, процентную ставку называют при этом ставкой наращения .
Антисипативными процентами называют проценты начисляемые по принципу скидки с конечной суммы задолжности называют учетной ставкой.
Дискретными процентами называют такой способ наращения, при кото ром время считают величиной дискретной.
Непрерывными процентами называют способ наращения, при котором время рассматривают как непрерывное.
Компаундинг — это процесс перехода от сегодняшней (т.е. текущей) стоимости капитала к его будущей стоимости.
Дисконтирование — это процесс определения сегодняшней (т.е. текущей) стоимости денег, когда известна их будущая стоимость. Применяется для оценки денежных поступлений (пибыль, проценты. Дивиденды) с позиции текущего момента.
Виды простых ставок
Любые проблемы, связанные с финансами, имеют множество нюансов. И это в полной мере относится к расчетам по формуле (1.1).
Причем в практических проблемах, связанных с расчетом процентов, эти нюансы в основном касаются определения длительности займа t. Отметим неко торые из них. Для этого еще раз напомним, что мы договорились считать единицей времени год.
В краткосрочном контракте по предоставлению кредита срок его дей ствия естественно измерять днями. Поэтому при выбранной единице вре мени длительность займа удобно записывать в виде
t=n/N (1)
где n — длительность контракта в днях, а N — число дней в году. При этом оказывается, что в разных странах мира сложилась своя практика, банковская и коммерческая, в отношении базы времени N . Возможны следующие четыре варианта:
N=360, N=3б5, N=365,25, N = 366.
из которых первый во многих странах называется коммерческим годом.
Сложные проценты
... через 6 лет. 1.3. Наращение процентов m раз в году. Номинальная и эффективная ставки В современных условиях проценты капитализируются, как правило, не один, а несколько раз в году — по ... проценты. Присоединение начисленных процентов к сумме базы начисления называют капитализацией процентов. Применим те же обозначения, что и в формуле наращения по простым процентам. В конце первого года проценты ...
Но выбор одного из этих вариантов еще не вносит полную ясность в расчет t поскольку не меньше подходов к определению числа n. Так, оно может быть точным числом дней от одной даты до другой, включаю щим или не включающим в себя границы. Хотя наиболее распространен ная практика определения числа дней ссуды по календарю такая: первый день не учитывается, а последний – учитывается . Но это же число мо жет получаться совсем по-другому. Например, когда рассматриваемый период (ссуды) разбивается на три части, две из которых — первая и тре тья — выражаются в днях, а средняя — точным числом месяцев, которые берутся равными 30 дням, или семестров, равных 90 дням.
Кстати, в Германии, Дании, Швеции год условно считается коммер ческим, а месяц — имеющим 30 дней. Также коммерческий год использу ется во Франции, Бельгии, Испании, Швейцарии, Югославии. Но здесь предпочитают рассчитывать точное число дней контракта по календа рю. Наконец, обычный год в 365 дней (или 366) и календарный расчет срока распространен в таких странах, как Португалия, США и Велико британия. При этом, скажем, в Англии , при банковских ссудах полгода приравниваются к 182 дням.
В банковской системе используют три способа расчета процентов:
Точеные проценты с точным числом дней ссуды или 365/365.
Обыкновенные проценты с точным числом дней ссуды или 365/360.
Обыкновенные проценты с приближенным числом дней ссуды или 360/360.
Вариант 360/365 на практике не применяется.
Формула наращения по простой процентной ставке
Пусть:
I — проценты за весь срок ссуды;
Банковский процент
... между кредитором и заёмщиком и выступает в форме определённой процентной ставки. Банковский процент, как и любая другая экономическая категория, имеет свою сферу функционирования и ... акта Республики Беларусь. 1. БАНКОВСКИЙ ПРОЦЕНТ 1.1 Сущность банковского процента, его функции Процент - это часть прибыли, которую заёмщик выплачивает кредитору за взятый в ссуду денежный капитал, он определяется ...
Р — первоначальная сумма долга;
S — наращенная сумма, или сумма в конце срока;
i — ставка наращения (десятичная дробь);
n — срок ссуды.
Каждый год процента составляют Рi.
Начисленные за весь срок про центы:
I=Pni (2)
Наращенная сумма:
S = Р + I = Р (1+ni) (3)
Это — формула простых процентов. Множитель — множитель наращения проема процентов.
Переменные ставки
Если предусмотрены изменяющиеся во времени процентные ставки, то наращенная сумма будет определяться следующим образом:
S = Р ( 1 +n 1 i 2 + n 2 i 2 + … +n m i m ) (4)
Где i k – процентная ставка в период k,
n k – продолжительность периода к.
В ряде практических приложений финансового анализа встает вопрос об определении первоначальной суммы долга по накопленной сунне, в зависимости от используемой ставки он решается путей использования мате матического дисконтирования или банковского учета.
Математическое дисконтирование
Математическое дисконтирование является точным формальным решени ем обратной задачи.
Р = S/(1+ni) (5)
Множитель:
1
1 + ni
называют дисконтным множителем .
Задача 1
Определить сумму, вложенную в коротко-срочные облигации доходностью 5% годовых на 7 месяцев, которые принесли дивиденды на 19000 рублей.
Решение
i = 0,05/12 = 0,0041 или 0,42 %
по формуле (5):
P= 19000/(1+7*0,0041) = 18464,5 рубля
Идея сложных процентов очень проста. В них, в отличие от простых про центов, существует период времени, по истечении которого проценты начисляются не только на имеющуюся в начале этого периода сумму, но и на накопившиеся к его концу проценты. Конечно, интервал этот может быть разным по длине, например, месяц или год. Но если уж он выбран, то является циклическим, т.е. на некотором промежутке ось времени раз бивается этими периодами, а равные части, как линейка на сантиметры. В то же время так же, как и простые проценты, сложные не могут не существовать !
Но если без простых процентов нельзя обойтись из-за соображений удоб ства в обращении или, скажем, ощущения справедливости линейной за висимости вознаграждения от суммы кредита и времени, то в случае сложных процентов основную роль играет наличие свободной конкуренции.
Формула наращения сложных процентов
S = P(1 + i) n (6)
Р — первоначальная сумма долга;
S — наращенная сумма, или сумма в конце срока;
i — ставка наращения (десятичная дробь);
n — срок ссуды.
Например,
Задача 2
Если положить на срочный вклад 100 000 под 60% годо вых и на два года, то в результате на этом вкладе окажется 220 000, если действует формула начисления простых процентов (3) и ставка за все это время не изменится:
S = 100 000(1+2*0,6) = 220 000.
А если через год снять имеющуюся на счету сум му 160000 и положить на такой же срочный вклад, но в другом банке, то через те же два года получится сумма 256 000 = 160 000 + 96 000, очевидно, на 36 000 большая. Но ведь первый банк не захочет потерять своего клиента-вкладчика и потому сразу предложит ему формулу(6): S = 100 000(1+0, 6) 2 =256 000.
Переменные процентные ставки
В некоторых случаях(каких) ставка может изменяться во времени, тогда формула начисления сложных процентов примет вид:
S = P(1 + i) n1 (1 + i) n2 … (1 + i) nk . (7)
Математическое дисконтирование
P = S/(1+i) n (8)
Р — первоначальная сумма долга;
S — наращенная сумма, или сумма в конце срока;
i — ставка наращения (десятичная дробь);
n — срок ссуды.
Задача 3
Банк предлагает 50% годовых. Каков должен быть первоначальный вклад, чтобы через три года иметь на счете 100 000?
Решение
По формуле (8):
P = 100 000 / (1+0,5) 3 = 29600.
Сравнение роста по сложной и простой процентной ставке
Сравним множители наращения по простой и сложным процентным ставкам. При сроке большем нуля и меньше года множитель наращения по простой процентной ставке превосходит множитель наращения по сложной:
(1+ni) > (1+i) n
При сроке больше года множитель наращения по сложной прцентной ставке больше множителя по простой:
(1+ni) < (1+i) n
При сроках, равных нулю и единице, множители наращения по сложным и простым процентам равны.
S
p 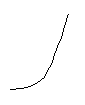
0 1 n время
Для наглядности рассмотрим таблицу «Простые и сложные проценты для капитала P =100 000»
|
года |
3% |
9% |
15% |
20% |
||||
|
Прост. |
Слож. |
Прост. |
Слож. |
Прост. |
Слож. |
Прост. |
Слож. |
|
|
1 |
3 |
3 |
9 |
9 |
15 |
15 |
20 |
20 |
|
5 |
15 |
16 |
45 |
54 |
75 |
101 |
100 |
149 |
|
10 |
30 |
34 |
90 |
137 |
150 |
305 |
200 |
519 |
|
15 |
45 |
56 |
135 |
264 |
225 |
714 |
300 |
1441 |
|
20 |
60 |
81 |
180 |
460 |
300 |
1537 |
400 |
3734 |
Насколько прогрессивна сложная процентная ставка, очевидно, ее более интенсивный рост при увеличении срока капитализации и доходности налицо.
Инфляция
Изменение стоимости за счет инфляции:
С= S*J (9)
C – номинальная стоимость,
S – реальная стоимость (та, которая бы была, если бы не было инфляции),
J – индекс инфляции, равный 1+ j,
j – процент инфляции.
Инфляция является цепным процессом и всегда учитывается по формуле сложного процента.
Таким образом инфляция пораждает такие понятия, как реальная и номинальная процентные ставки. Под реальной процентной ставкой понимают ставку процента i , который бы капитализировался не будь инфляции j. Под номинальной процентной ставкой h понимают ставку, применяемую инфляционным деньгам. Эти ставки (для сложных процентов) соотносятся:
1+h = (1+i) (1+j), (10)
откуда получаем
h = i + j + ij. (11)
Часто последним членом пренебрегают, т.е. :
h=i +j, (12)
рассчитанная таким образом номинальная ставка не сильно отличается от рассчитанной по формуле (12), но только в случае если инфляция не существенна. Если темпы инфляции высоки, то пренебрегать последним членом нельзя.
- Балабанов И.Т. «Основы финансового менеджмента», М: «Финансы и статистика» 2001;
- Жуленев С.В. «Финансовая математика» изд. МГУ 2001;
- Комзолов А.А., Максимов А.К., Миловидов К.Н. «Финансово-математические модели» изд. «РГУНГ им .И.М. Губкина» 1997.
1 В России именно такой подход, хотя он и звучит иначе: первый и последний день считаются за один день,