Оптимизационное моделирование в экономике

метки: Изделие, Задача, Решение, Работа, Ограничение, Модель, Неделя, Полка

• Организационный момент – 2 мин;
• Изложение нового материала – 13 мин;
• Закрепление нового материала (самостоятельная практическая работа) – 25 мин;
• Домашнее задание – 2 мин;
• Итоги урока – 3 мин.

Ход 1-го урока: презентация .

1. Перекличка. Объявление темы и цели занятия

Человеку практически ежедневно приходится сталкиваться с проблемой принятия решений для достижения тех или иных целей. В экономике целями могут быть увеличение прибыли, снижение затрат, повышение производительности труда, рациональное использование оборудования и материалов, повышение эффективности инвестиций и многое другое. Для решения таких задач очень широко используется метод Оптимизационного моделирования, с которым мы сегодня и познакомимся

2. Новая тема.

Слайд 2. Давайте выясним, что же такое “оптимизация”. Заглянем в Википедию.

В математике это – нахождение оптимума (максимума или минимума) функции при выполнении некоторых ограничений

В информатике – процесс модификации системы для улучшения ее .

За своей сущностью задача оптимизации – это математическая модель определенного процесса производства продукции, его распределение, хранение, переработки, транспортирования, покупки или продажи, выполнение комплекса сервисных услуг и т.д. Это обычная математическая задача типа: Дано/Найти/При условии, но которая имеет множество возможных решений. Таким образом, задача оптимизации – задача выбора из множества возможных вариантов наилучшего, оптимального.

Слайд 3. Объектами планирования могут быть самые разные системы: деятельность отдельного предприятия, отрасли промышленности или сельского хозяйства, региона, наконец, государства.

целевой функцией.

Слайд 5. Цель исследования состоит в нахождении экстремума этой функции и определении значений параметров, при которых этот

Слайд 6. Если целевая функция нелинейна, то она имеет экстремумы, которые находятся определенными методами. Однако часто целевая функция линейна и, соответственно, экстремумов не имеет. Задача поиска оптимального режима приобретает смысл только при наличии определенных ограничений на параметры.

Мы будем рассматривать только решение линейных задач с использованием оптимального планирования.

Слайд 7. Постановка задачи планирования выглядит следующим образом:

• имеются некоторые плановые показатели: х, у и другие;
• имеются некоторые ресурсы: Rl, R2 и другие, за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены;
• имеется определенная стратегическая цель, зависящая от значений х, у и других плановых показателей, на которую следует ориентировать планирование.

определить

Содержание, значение и задачи финансового планирования

... области финансов 2.2 Задачи финансового планирования Основными задачами финансового планирования на предприятии, на мой взгляд, явля­ются: обеспечение необходимыми финансовыми ресурсами производственной, инвестиционной и финансовой деятельности; определение ... Румянцева Е.Е., Ковалева А.М., Поляка Г.Б. и многих других. 1. Виды планов и их содержание В приложении к социально-экономическим системам, ...

Примеры.

1. Пусть объектом планирования является детский сад. Ограничимся лишь двумя плановыми показателями: числом детей и числом воспитателей. Основными ресурсами деятельности детского сада являются размер финансирования и площадь помещения. А каковы стратегические цели? Естественно, одной из них является сохранение и укрепление здоровья детей. Количественной мерой такой цели является минимизация заболеваемости воспитанников детского сада.
2. Планирование экономической деятельности государства. Безусловно, это слишком сложная задача для того, чтобы нам с ней полностью разобраться. Плановых показателей очень много: это объем производства различных видов промышленной и сельскохозяйственной продукции, план подготовки специалистов, количество вырабатываемой электроэнергии, размер зарплаты работников бюджетной сферы и многое другое. К ресурсам относятся: количество работоспособного населения, бюджет государства, природные ресурсы, энергетика, возможности транспортных систем и пр. Как вы понимаете, каждый из этих видов ресурсов ограничен. Кроме того, важнейшим ресурсом является время, отведенное на выполнение плана. Вопрос о стратегических целях довольно сложный. У государства их много, но в разные периоды истории приоритеты целей могут меняться. Например, в военное время главной целью является максимальная обороноспособность , военная мощь страны. В мирное время в современном цивилизованном государстве приоритетной целью должно быть достижение максимального уровня жизни населения .

Кроме того, иногда интересует не конкретный результат, а минимально или максимально возможный. Например, как минимизировать затраты на содержание персонала или максимизировать прибыли от реализации продукции? Как найти нескольких параметров, обеспечивающих некоторый наперед заданный результат.

Слайд 8. Рассмотрим пример.

Фирма производит две модели А и В сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки. Для каждого изделия модели А требуется 3 м ² досок, а для изделия модели В – 4 м² . Фирма может получать от своих поставщиков до 1700 м² досок в неделю. Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В – 30 мин. В неделю можно использовать 160 ч машинного времени. Сколько изделий каждой модели следует выпускать фирме в неделю, еcли каждое изделие модели А приносит 2 долл. прибыли, а каждое изделие модели В – 4 долл. прибыли?.

Решение состоит из трех этапов:

1. Разбор задачи и создание математической модели
2. Составление формальной модели
3. Создание компьютерной модели, которую можно выполнить в среде ЭТ Excel или в среде программирования

математическую

Обозначим: х – количество изделий модели А, выпускаемых в течение недели, у – количество изделий модели В.

Линейная модель многоотраслевой экономики

... количество про­дукции, реализованной на момент времени t; тогда Рассмотрим модель рынка с прогнозируемыми ценами. В простых моделях ... задачу нахождения экстремума функции нескольких переменных, возникающую в экономике. Прибыль от производства разных видов товара &nbs ... Гаусса является поистине универсальным в решении систем линейных алгебраических уравнений. Мы продемонст­рируем применение этого ...

Прибыль от этих изделий равна (2х + 4у) долл. Эту прибыль нужно максимизировать. Функция, для которой ищется экстремум (максимум или минимум), носит название целевой функции.

Беспредельному увеличению количества изделий препятствуют ограничения.

Ограничено количество материала для полок, отсюда неравенство (3x + 4y≤1700).

Ограничено машинное время на изготовление полок. На изделие А уходит 0,2 часа, на изделие В – 0,5 часа, а всего не более 160 ч, поэтому (0,2x + 0,5y ≤ 160).

Кроме того, количество изделий – неотрицательное число, поэтому х > 0, у > 0 и целое

Слайд 9 . Формально эта задача оптимизации записывается так:

Слайд 10–25 . Компьютерная модель. Решение задачи в Excel.

1. Создайте новую рабочую книгу, сохраните ее под именем Chll.xls в своей папке.

2. Дайте первому листу имя «Полки».

3. Введите в ячейки рабочего листа информацию (рис.1).

Ячейкам В2 и ВЗ присвойте имена х и у. В ячейках С6, С9 и С10 представлены формулы, занесенные в соответствующие ячейки столбца В.

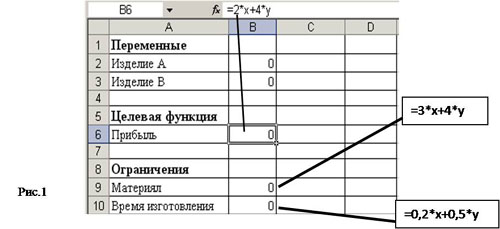
4. Выделите ячейку ( B6 ), в которой вычисляется целевая функция, и вызовите Решатель («Сервис/ Поиск решения»).

В диалоговом окне в поле ввода «Установить целевую ячейку:» уже содержится адрес ячейки с целевой функцией $В$6 .

5. Установите переключатель: «Равной максимальному значению».

$В$2:$В$3

7. Перейдите к вводу ограничений. Щелкнем кнопку «Добавить». Появится диалоговое окно «Добавление ограничения».

8. В поле ввода «Ссылка на ячейку:» укажите $В$9 .

9. Правее расположен выпадающий список с условными операторами (раскройте его и посмотрите).

Выберем условие <=.

10. В поле ввода «Ограничение:» введите число 1700. (Рис. 2)

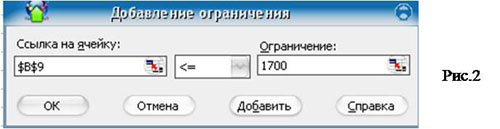
$В$10<=160

12. Ввод ограничений закончен, поэтому нажмем «ОК».

$В$10<=160

14. Щелкните кнопку «Параметры». Окажемся в диалоговом окне «Параметры поиска решения». Чтобы узнать назначение полей ввода этого окна, щелкнем кнопку «Справка». Менять ничего не будем, только установим два флажка: «Линейная модель» (так как наши ограничения и целевая функция являются линейными по переменным х и у) и «Неотрицательные значения» (для переменных х и у). Щелкнем «ОК» и окажемся в исходном окне.

Контрольная работа: Валютные ограничения и валютный риск

... 1.2. Цели валютных ограничений: Валютные ограничения как разновидность валютной политики преследуют следующие цели: 1) выравнивание платежного баланса; 2) поддержание валютного курса; 3) концентрация валютных ценностей в руках государства для решения текущих и ...

Самостоятельно добавьте ограничения, что переменная X и Y – целые

15. Полностью подготовив задачу оптимизации. Нажимаем кнопку «Выполнить».

16. Появляется диалоговое окно «Результаты поиска решения». В нем читаем сообщение «Решение найдено. Все ограничения и условия оптимальности выполнены.» На выбор предлагаются варианты: «Сохранить найденное решение» или «Восстановить исходные значения». Выбираем первое. Можно также вывести отчеты: по результатам, по устойчивости, по пределам. Выделим их все, чтобы иметь представление о том, какая информация в них размещена.

17. После нажатия «ОК.» вид таблицы меняется: в ячейках х и у появляются оптимальные значения. Числовые данные примера специально подобраны, поэтому в ответе получились круглые цифры: изделие А нужно выпускать в количестве 300 штук в неделю, а изделие В – 200 штук. Соответственно пересчитываются все формулы. Целевая функция достигает значения 1400. (Рис. 5)

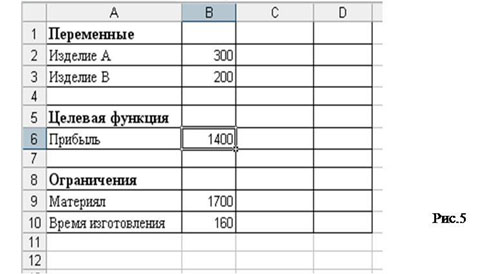
3. Практическая работа. Создание и исследование модели.

заготовка .

4. Домашняя работа. Учебник §5.10, записать в тетрадь 2 этапа создания модели “Способы раскроя заготовки”.

5. Подведение итогов урока.

План 2-го урока:

• Организационный момент – 2 мин;
• Визуальная проверка домашней работы в тетради и выполнение практической работы – 10 мин;
• Самостоятельная практическая работа по вариантам – 20 мин;
• Разбор решения самостоятельной работы (вывод на электронную доску по одному решению из двух вариантов) – 8 мин;
• Домашнее задание. Итоги урока – 5 мин.

Ход 2-го урока:

1. Перекличка. Объявление цели занятия.
2. Выполнение самостоятельной работы по вариантам.

   Вариант 1 .

   Вариант 2 .

3. Разбор решения самостоятельной работы.
4. Домашняя работа по вариантам . (Желательно домашнюю работу разместить на сайте или распечатать ее на листках.)
5. Подведение итогов урока.

Литература:

1. Н.Д. Угринович “Информатика и информационные технологии” 10–11 класс, М., БИНОМ. Лаборатория знаний.
2. С. М. Лавренов Excel. “Сборник примеров и задач” (Диалог с компьютером).

   М., Финансы и статистика, 2003.

3. Интернет: сайт Википедия.
4. http://ru.wikipedia.org/wiki/%D0%9E%D0%BF%D1%82%D0%B8%D0%BC%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D1%8F
5. Леоненков А. Решение задач оптимизации в среде MS Excel – СПб.: БХВ – Петербург, 2005. – 704 с.. ил.
6. Сдвинков О.А. Математика в MS Excel 2002 – М., Солон-Пресс, 2004–192 с.. ил.
7. http://citforum.ru/pp/excel72.shtml
8. http://math.semestr.ru/example.html
9. Гарнаев А.Ю. Использование MS Excel и VBA в экономике и финансах. – СПб.: БХВ, 2000. – 336 с.: ил.

6.02.2013

Контрольная работа: Значение государственной инвестиционной политики ...

... за рубежа. Поэтому цель данной работы – рассмотреть иностранные инвестиции как фактор экономического развития. 1. Государственная инвестиционная политика: понятие, значение. В деятельности любого хозяйствующего субъекта наступают ... по сравнению с головной компанией является меньшим фактором влияния на размещение производства на данном континенте. Издержки производства являются решающими и для ...